Concept and Form:
The Cahiers pour l’Analyse
and Contemporary French Thought

This project is funded by an Arts and Humanities Research Council (AHRC) research grant and is supported by the Centre for Research in Modern European Philosophy (CRMEP) and Kingston University's Faculty of Arts and Social Sciences.

1. Triple articulation du processus logique

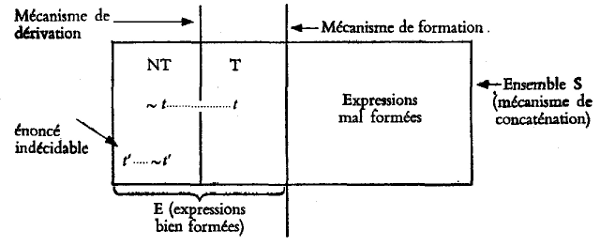
La théorie de la logique se rapporte aux modes de production d’une division dans l’écriture linéaire; soit la dichotomie d’un ensemble structuré d’énoncés ‘introduits’ dans le mécanisme dernier au titre de matière première (déjà travaillée).

Il en résulte immédiatement que le requisit unique à quoi doit obéir le fonctionnement du mécanisme est qu’au bout du compte quelque chose soit en effet coupé; que des écritures soient mécaniquement réparties en deux classes disjointes, désignées, par allusion au mécanisme le plus souvent utilisé: classe des énoncés dérivables, classe des énoncés non-dérivables.

La définition classique de la consistance absolue d’un système: qu’au moins une expression bien formée ne soit pas dérivable dans le système, désigne précisément cette exigence minimale. Sa transgression équivaut à considérer un mécanisme logique qui ne produit rien, la production n’étant en l’occurrence rien d’autre que la division effective des matériaux sur lesquels on opère.

A y regarder de plus près, on constate que cette division finale implique l’opération successive de trois mécanismes ordonnés. Car avant d’être répartis, les syntagmes doivent être formés, puis triés, aucun système de dérivation ne pouvant les soumettre tous à son principe de division (ce qui veut simplement dire qu’une machine spécialisée possède une entrée où ne peuvent être introduits que des matériaux spécifiques, préalablement usinés).

Nous aurons donc à distinguer les mécanismes de concaténation, de formation, et de dérivation.

Toute dissimulation de l’autonomie du second mécanisme - par rapport au troisième - a pour effet la perte de l’essence même : la fonction productrice du processus logique.³ Et rien n’est plus important que de parcourir dans leur ordre les machineries de la logique.

a) Concaténation: La matière absolument première du processus logique [152] lui est fournie par une sphère particulière de la production technique, l’écriture. Il s’agit en effet d’un stock de marques graphiques, séparables et indécomposables, formant un ensemble fini ou au plus dénombrable que nous appellerons l’alphabet.

Le premier mécanisme ‘reçoit’ ces marques dont il compose des suites finies (juxtaposition linéaire avec répétitions éventuelles). Il est monté pour produire toutes les suites finies de cette espèce, et ce sont donc elles que nous trouvons à la sortie du mécanisme. Soit S cette production.

b) Formation: Le deuxième mécanisme opère sur S, et en réalise de proche en proche une dichotomie parfaite, qui sépare sans reste les suites ‘acceptées’ par la machine des suites rejetées. On appelle expressions bien formées les expressions acceptées, mal formées les autres.⁴

Les opérateurs (les ‘pièces’ ) de ce mécanisme sont les règles de formation, qui prescrivent aux concaténations acceptables certaines configurations: par exemple, la machine dite ‘calcul des prédicats avec égalité’ pourra accepter les suites I (x, x) et non-I (x, x) mais rejettera la suite x (I, x).

Par une dangereuse tolérance sémantique, on appelle souvent les énoncés rejetés des non-sens.

L’ensemble des règles de formation constitue la syntaxe.

Remarquons tout de suite que si, comme l’indique en apparence le célèbre théorème de Gödel, la dichotomie dernière (celle du troisième mécanisme) ne peut, pour une machine ‘forte’ , se faire sans reste⁵ - car il y a toujours des énoncés indécidables -, la possibilité même de ce résultat présuppose l’existence d’un mécanisme dichotomique sans reste: celui qui fournit au mécanisme démonstratif sa matière première, les expressions bien formées. Les apories de la dérivation sont assignables sous la condition d’une syntaxe parfaite.

L’ordre signifiant refendu, marqué par ce dont il manque, n’est exhibé [153] que dans sa différence à un ordre autonome effectivement fermé, c’est-à-dire intégralement décidable (celui de la formation des syntagmes). En ce sens, on ne peut soutenir que la déchirure ou l’itération compulsive soient le prix inévitable de la fermeture. Il faut dire: l’existence d’un mécanisme fermé infaillible conditionne celle d’un mécanisme dont on puisse dire qu’il est infermable, et donc intérieurement limité.

La monstration d’une suture présuppose l’existence d’une forclusion.

Quoi qu’il en soit de cette anticipation théorique, retenons qu’à la sortie du mécanisme syntaxique, nous trouvons l’ensemble des expressions bien formées, soit E.

c) Dérivation: Le troisième mécanisme opère sur E, et il est généralement monté pour en produire:

1: Une dichotomie parfaite, entre Thèses (ou énoncés dérivables) et non-Thèses (énoncés indérivables),

2: Un certain type de liaison fonctionnelle entre les moitiés.

Cette deuxième condition est capitale. Si l’exigence de dichotomie était la seule, les mécanismes logiques classiques (par exemple une formalisation de l’arithmétique) n’auraient aucun défaut: il est bien vrai que tous ces mécanismes séparent sans reste les expressions bien formées en dérivables et non dérivables, en thèses (T) et non-thèses (NT).⁶

Un énoncé indécidable, comme celui que construit Gödel, n’est évidemment pas un énoncé qui ne serait ni démontrable ni indémontrable (ce qui n aurait aucun sens). Le centre de la preuve de Gödel est au contraire atteint quand on montre que cet énoncé n’est pas démontrable. Il est donc bien assigné à l’une des deux moitiés.

Un énoncé indécidable n’est pas le reste d’une coupure, mais un énoncé tel que ni lui ni sa négation ne sont dérivables. Un tel énoncé est certes irréfutable (réfutation = démonstration de la négation). Mais il est explicitement indémontrable. Il y a bien partage sans reste entre le dérivable et le non-dérivable: mais l’énoncé de Gödel et sa négation sont dans la même moitié.

Tout repose ici sur un opérateur syntaxique spécial, et la structure qu’il commande, l’opérateur de négation.

[154]

On ne peut donc soutenir que le théorème de Gödel signifie: toute dichotomie laisse un reste. Ou: toute dualité implique un tiers disjoint décentré par rapport à la règle qui ordonne intérieurement chaque terme du couple. Cette lecture (fréquente) du théorème est une importation métaphysique. En réalité, le problème tient aux conditions structurales particulières imposées au troisième mécanisme logique en surcharge de sa fonction séparatrice: ce que résume ci-dessus notre condition 2.

On exige en effet qu’il y ait dans l’alphabet un opérateur (négation ou tout autre: le sens intuitif de la négation est ici un obstacle) tel que, si un énoncé appartient à une moitié (t∈T ou t∈NT) alors, l’énoncé obtenu en lui appliquant l’opérateur, soit ~ ⁷, est dans l’autre moitié (~t∈NT ou ~t∈T).

Ce qui est ici originairement en question n’est pas la coupure comme telle, mais une fonction de liaison entre les moitiés séparées. La limite gödélienne ne s’attache pas à la dichotomie. Elle concerne au contraire l’unité-de-correspondance des parties disjointes.

L’énoncé de Gödel signifie: soit la liaison fonctionnelle qui rapporte tout énoncé à sa négation: t … ~t. Il n’y a pas de dichotomie effective telle que toutes ces liaisons soient coupées.

Sans doute peut-on espérer chasser de T (énoncés dérivables) toutes les liaisons t ... ~ t; sans quoi le système serait inconsistant. Mais on montre alors qu’il en reste toujours dans NT: précisément celles qui concernent les énoncés indécidables.

Nous avons donc à considérer ici une déchirure de structure, et non une dichotomie. La clé de la limitation tient paradoxalement à ce qu’on impose au mécanisme séparateur de n’être pas parfait: de préserver le concept d’un rapport réversible entre les moitiés. De sorte que la limitation, loin d’attester que figure dans un espace produit par division la trace de la déchirure dont il résulte, montre plutôt qu’on n’y peut produire indéfiniment le signe de l’autre; qu’en certains lieux, la trace est effacée; qu’un mécanisme [155] fort impose une division complète dans le rejet qu’elle fait, en chacune de ses parts, de certaines marques du vieux Tout.

L’indécidable n’est pas la suturation du manque, mais la forclusion de ce qui manque par l’échec à produire, dans le dérivable, tout le non-dérivable en tant que nié.

La limitation signifie: il existe en un point, entre les parties T et NT, une distance sans concept: celle qui fait figurer, dans l’espace des non-thèses, un énoncé dont la négation ne s’inscrit pas dans l’espace des thèses, et qui est donc non-rapporté à cet espace. Le théorème de Gödel est le lieu de plus grande efficace de la séparation, non le lieu de son échec.⁸

Si donc les théorèmes de ‘limitation’ résultent des conditions d’imperfection assignées au mécanisme dichotomique, il nous faut remanier le concept de ce dernier pour y intégrer ces conditions. Nous dirons:

La logique est un mécanisme triplement articulé (concaténation, syntaxe, dérivation) qui produit une division terminale dans l’écriture linéaire, et qui est tel qu’étant donné un syntagme convenable on doit pouvoir:

i) Le distribuer dans une des deux moitiés (T ou NT)

ii) Construire un syntagme mécaniquement obtenu à partir du premier par adjonction d’un foncteur (généralement nommé négation), et tel que si le premier est dans une moitié, le second est dans l’autre.

La condition i est idéalement⁹ satisfaite par les mécanismes classiques (théorie des ensembles ou formalisation de l’arithmétique). La seconde ne l’est que par des mécanismes faibles: un mécanisme fort coupe trop bien.

2. Nullité de la chose - Identité des marques

La description du mécanisme logique nous autorise à questionner la construction en ce domaine du concept de suture, et nous permet de déterminer exactement la fonction méta-théorique du zéro.

Annonçons dès l’abord nos thèses:

1) Le concept d’identité n’a valeur que pour les marques. La logique n’a nulle part à connaître d’une chose identique à soi, fût-ce au sens où la ‘chose’ serait l’objet du discours scientifique.

2) Le concept de vérité est un indicateur idéologique, résumant-dissimulant des concepts scientifiques de sélection et de division. Il désigne globalement un mécanisme différencié.

3) Le zéro n’est pas dans un système la marque du manque, mais le signe [156] où s’abrège le manque d’une marque. Ou plutôt: l’indication, dans un ordre signifiant, de ce qu’une écriture est présente dans la moitié rejetée d’un autre ordre.

4) Le signifiant logico-mathématique n’est suturé qu’à lui-même. Il est indéfiniment stratifié.

5) En logique, tout manque qui n’est pas un signifiant n’a aucun signifiant: il est forclos.

6) Le concept de suture n’articule pas sur le manque le signifiant en général. Sa pertinence requiert une condition spécifique dans le signifiant. Et cette condition n’est pas construite par la psychanalyse, mais par le matérialisme historique: seul le signifiant idéologique est suturé.

Les discussions par J.-A. Miller de Frege¹⁰ comme de Boole, par Lacan du théorème de Gödel ou de la sémantique de l’implication, ont cette ambiguïté qu’elles déploient simultanément, et sans distinction, ce qui relève de la construction effective d’un mécanisme logique, et ce qui relève du discours (idéologique) par quoi les logiciens se représentent cette construction.

Ainsi faut-il se garder de comprendre à l’intérieur du procès logique toute retraduction de l’instance articulatoire des signes dans le lexique de la subsomption. Cette notion, close dans la relation référente (spéculaire), comme d’ailleurs celle, connexe, de dénotation, dissimule l’essence strictement fonctionnelle des renvois intérieurs au mécanisme logique.

Rien ici n’autorise la détermination d’un objet. La chose y est nulle: aucune écriture ne peut l’objectiver.

On ne peut trouver dans cet espace mécanique que des fonctions réversibles de système à système, de marque à marque: des dépendances mécaniques de mécanismes. La sémantique elle-même n’entre dans la logique que pour autant qu’elle travaille entre deux ordres signifiants logicomathématiques, et sous la condition que les fonctions de correspondance entre ces ordres soient elles-mêmes logico-mathématiques.¹¹

La chose ni l’objet n’ont pas chance d accéder ici à plus d’existence que leur exclusion sans traces.

Il en résulte que l’exigence leibnizienne d’identité-à-soi, dont dépend que la vérité soit sauve, n’est intra-logique (théorique) que si elle concerne l’identité des marques. Elle postule, par une confiance inaugurale en la permanence des graphies, l’existence d’une application ‘identique’ de l’ordre signifiant sur lui-même, qui en préserve la structure.

[157]

C’est au demeurant la science entière qui tient l’identité-à-soi, non pour un prédicat de l’objet, mais pour un prédicat des marques. La règle vaut certes pour les faits d’écriture de la Mathématique. Elle vaut tout aussi bien pour les inscriptions d’énergie de la Physique. Comme l’a admirablement montré Bachelard, la seule règle de substitution proprement physique concerne les opérateurs artificiels: “Le principe d’identité des appareils est le véritable principe d’identité de toute science expérimentale.”¹² C’est l’invariance technique des traces et des instruments qui se soustrait à toute ambiguïté dans les substitutions.

Ainsi déterminée, la règle de l’identité-à-soi ne souffre aucune exception, et ne tolère pas l’évocation, même rejetée, de ce qui s’y dérobe. Le non-substituable à soi-même est un impensé radical, dont le mécanisme logique ne porte pas trace. Impossible d’en produire l’évanescence, l’oscillation miroitante, comme chez Frege de la chose non-identique à elle-même fantomatiquement (idéologiquement) convoquée, puis révoquée, aux fins d’assignation du zéro. Le non-substituable à soi-même est forclos sans recours ni marque.

Cependant on construit dans les systèmes logiques un prédicat homonyme: il existe des ‘calculs de l’identité’ , où se marque la non-identité.

Pour éviter les glissements de langage, nous conviendrons de nommer ‘égalité’ ce prédicat, noté I(x, y) (qui se lit d’ordinaire: x est identique à y).

L’homonymie usuelle dissimule, nous allons le montrer, un rapport de présupposition qui fait apparaître une fois de plus la priorité du forclos.

Si l’on considère par exemple un calcul du premier ordre (où il est impossible de quantifier les prédicats), on définira implicitement la constante prédicative d’égalité I par deux axiomes¹³:

- I(x, x)   (Reflexivité totale)

- I(x, y) ⊃ [A(x) ⊃ A(y)]

On pourrait croire que l’axiome de reflexivité thématise dans les écritures du calcul (à la sortie du mécanisme syntaxique) l’identité-à-soi fondatrice d’une lettre quelconque. Il n’en est rien: ce que nous avons convenu d’appeler l’égalité-à-soi d’une variable n’est pas l’identité à soi de toute marque. La meilleure preuve en est que cette égalité admet la construction de sa négation: ~I(x, x) est une expression bien formée du système, une expression lisible.

On aurait cependant tort d’imaginer que ~ I(x, x) (à lire: x n’est pas égal - ou identique - à soi) marque dans le système, place dans le mécanisme, l’impensable non-identité-à-soi du signe, et qu’une telle expression (correcte) organise la suturation au calcul de cet impensable. Au contraire l’existence [158] signifiante de ~I(x, x), loin de marquer l’impensé, suppose son fonctionnement sans marque; il faut qu’on ne puisse pas penser que x, en tant que marque, est ‘autre’ que x, même marque autrement placée, pour que soit logiquement produit cet énoncé. La simple convocation-révocation d’une non-identité à soi de x, le miroitement de son autodifférence, suffira à anéantir l’existence scripturale du calcul entier, et tout spécialement des expressions, comme ~I(x, x), où x est en double occurrence.

La production du concept logique d’égalité et de non-égalité à soi présuppose la forclusion du non-identique à soi scriptural. Le manque de l’égal s’édifie sur l’absence absolue du non-identique.

Sans doute la structure d’un calcul de l’identité implique-t-elle généralement la dérivation de la thèse: ~I(x, x): il est faux que x ne soit pas égal à x. Mais cette ‘négation’ , en fait de manque, ne marque rien d’autre que le rejet (la présence) dans l’autre moitié (celle des non-thèses) de l’énoncé ~I(x, x), produit identiquement par le mécanisme syntaxique. Aucune absence n’est ici convoquée qui ne soit la distribution dans une classe plutôt que dans sa complémentaire, et selon les règles positives d’un mécanisme, de ce que ce mécanisme reçoit des productions d’un autre.

Ce qui nous permet de rapporter sans infiltration idéologique le concept d’identité au concept de vérité.

Rien n’y transpire de la chose, ni de son concept.

Mais ‘la vérité est’ , pure désignation commode d’un complexe opératoire, signifie, s’il faut y pointer l’identité et l’égalité:

Identité: La logique soutient ce rapport à l’écriture qu’elle n’en peut recevoir que les marques attestées dans la chaîne comme partout substituables à elles-mêmes. Au vrai, n’importe quelle marque, dont il appartient à la technique (extérieure) des graphies de fonder l’invariable reconnaissance.

Égalité: Il existe un ordre signifiant (un mécanisme de dérivation) dont les contraintes sélectives sont telles que sont distribués dans des moitiés différentes les énoncés I(x, x) et ~I(x, x).

Si l’on veut considérer, dans une perspective plus proprement logistique, que la production du mécanisme-3 est l’ensemble des thèses dérivables, on dira: le mécanisme est monté de telle sorte qu’y soit produit I(x, x) et rejeté ~I(x, x).

Ces deux écritures cependant sont antérieurement produites dans la même moitié (celle des expressions correctes) par un mécanisme-2 (une syntaxe). A partir de quoi seulement on peut donner sens au rejet de l’une d’entre elles par le mécanisme de dérivation.

Le non-égal-à-soi n’est ici exclu que sous la condition d’avoir à se placer dans un ordre signifiant autonome, sédimentairement organisé ‘en dessous’ de celui qui ne lui fait plus place.

Préserver à tout prix, en ce point, la corrélation de l’égal à soi et du vrai reviendrait à dire: la vérité, c est le système des contraintes qui différencient [159] le mécanisme-3, produisant le seul énoncé I(x, x), du mécanisme-2, où sont produits simultanément I(x, x) et ~I(x, x).

L’égal-à-soi comme salut de la vérité se réduit à n’être qu’une différence, par effet retiré, entre syntaxe et dérivation: entre matière première et produit. Plus exactement: entre deux mécanismes de sélection dont le second est plus fin que le premier.

3. Marque du manque, ou marque manquante?

Nous pouvons désormais risquer le Zéro.

Introduit par voie de définition, le zéro est un symbole abréviateur, valant pour une écriture produite par un mécanisme-2.¹⁴ Il s’agit d’une abstraction (d’une construction de prédicat à un argument) sur relation.

Adoptons provisoirement le langage ‘ensembliste’ de Frege.

Étant donnée une relation quelconque entre variables d’individu, soit R (x, y), on peut construire la classe des x qui satisfont R (x, x), et considérer l’appartenance à cette classe comme une propriété, un prédicat: le prédicat “être lié à soi-même par la relation R.” On a ainsi procédé à l’abstraction de la reflexivité sur la relation R.

Convenons de noter Ar⋅R le nouveau prédicat. Ar⋅R(x) ‘signifie’ : x a la propriété d’être lié à soi-même par la relation R.

Ces considérations, qui reposent sur un concept ‘intuitif’ de la classe, doivent maintenant être abandonnées, car elles sont étrangères au mécanisme logique: elles concernent la pédagogie idéologique du système.

En vérité, nous disposons simplement d’une règle syntaxique inhérente à un M₂, qui nous permet:

a) De construire, à partir d’un prédicat à deux variables (soit R), l’écriture acceptée Ar⋅R.

b) De traiter cette écriture exactement comme n’importe quel autre prédicat à une variable (ce qui nous autorise par exemple à écrire Ar⋅R(x) etc.).

L’abstraction est donc ici une règle permettant la formation mécanique d’un prédicat à un argument à partir d’un prédicat à deux arguments.

Cette abstraction peut naturellement opérer sur la relation I(x, y), dite relation d’identité. Comme un axiome du calcul de l’identité est précisément I(x, x), le M₃ de ce calcul dérivera trivialement l’énoncé (∀x)(Ar⋅I(x)), soit: tout x est lié à lui-même par la relation I.

Mais l’abstraction de reflexivité peut aussi bien être faite sur la relation de non-égalité: I(x, y), puisque cette écriture est produite par M₂.

On obtient ainsi une des définitions possibles du prédicat zéro.

0 = Ar⋅~I

[160]

0(x) pourra se lire: x est un zéro; il a la propriété de n’être pas égal à soi-même.

Satisfaire 0(x) - être un zéro - n’empêchera nullement le signe x, comme le signe 0, d’être partout substituables à eux-mêmes: identiques, ils le demeurent, si même ils supportent, ou nomment, la non-égalité (identité) à soi.¹⁵

Dire qu’ainsi défini le zéro ‘vise’ un objet non-identique à soi, ou qu’il est le prédicat du vide, convoque au point où ne se tiennent que des substitutions d’écritures la lecture métaphysique de l’Être et de son Plein.

Car l’écriture ~I(x, x) ne se tient à la place de rien d’autre, ni ne marque la place d’un rien.

Quant au zéro, il vient partout où se tient ce à quoi il équivaut par convention scripturale, soit Ar⋅~I. Il est construit positivement par M₂.

Appelons mécanisme-4 un système logique qui adjoindrait à M₃ la constante prédicative (le nom propre) 0, telle que ci-dessus définie. De quel manque cette adjonction pourrait-elle être la marque dans l’ordre signifiant ainsi désigné?

M₃, nous l’avons vu, rejette l’écriture I(x, x), et dérive l’écriture I(x, x). Ne faut-il pas considérer que le prédicat zéro marque dans le non-rejeté de M₄ ce qui a été rejeté dans M₃? N’est-il pas le prédicat satisfait par ‘aucun’ terme?

Au vrai, ces descriptions sont étrangères à la théorie logique. Le zéro est simplement une écriture acceptée par M2 et introduite, assortie de certaines règles d’emplois, dans M₄.

Si l’on veut cependant penser le lien du zéro à la non-figuration de ~I(x, x) dans la dérivation de M₃, il y faut un usage quelque peu allégorique des concepts. Mais il est recevable de dire: Le zéro marque dans M₄ (sous forme prédicative), non le manque d’un terme à satisfaire la relation, mais une relation manquante dans M₃: la relation ~I(x, x). Il faut ajouter aussitôt: si la relation peut manquer dans M₃, c’est en tant qu’elle figure dans M₂.

Jeu d’apparitions et disparitions entre ordres signifiants successifs et jamais exposé à la convocation d’un manque dans l’objet ni la chose.

Système de différences entre systèmes, réglé par des substitutions, des [161] équivalences et des retraits: marque manquante, jamais marque du manque.

Ce n’est pas un blanc dont le zéro nomme la place, mais la biffure d’une trace: il laisse visible sous sa marque (Ar⋅~I) l’autre marque (~I(x, x)) telle que rejetée par la dérivation.

Le zéro est la marque (dans M₄) d’une marque (dans M₂) manquante (dans M₃).

En deçà de la chaîne signifiante, si elle est scientifique, il n’y a jamais que d’autres chaînes. Si le signifiant se suture, c’est à soi. C’est de soi qu’il manque à chacun de ses niveaux: il règle ses manques sans sortir de soi. Le signifiant scientifique n’est pas suturé ni refendu, mais stratifié.¹⁶ Et la stratification révoque l’axiome par quoi Miller, dans un autre texte¹⁷, caractérise la forclusion: le manque d’un manque est encore un manque. Non, si ce qui vient à manquer fut toujours déjà marqué: dès lors l’interstice est assez nommé par la différence productrice des strates. Les points d’arrêt sont toujours prescrits.

4. Le supplice de la philosophie

Faut-il donc annuler le concept de suture? Il s’agit au contraire de lui prescrire sa fonction en lui assignant son domaine.

De ce qu’un ordre signifiant, la science, existe, stratifié, tel qu’aucun manque n’y est marqué qu’on ne puisse découvrir marque lui-même dans l’ordre sous-jacent dont se différencie le premier, résulte l’exception. La science ne tombe pas sous le concept de la logique du signifiant. Au vrai, c’est de n’y pas tomber qui la constitue: la coupure épistémologique doit être pensée sous les espèces irreprésentables de la désuturation.

En sorte qu’il n’y a pas de sujet de la science. Stratifiée à l’infini, réglant ses passages, la science est l’espace pur, sans envers ni marque ou place de ce qu’elle exclut.

Forclusion, mais de rien, on la peut dire psychose d’aucun sujet. Donc de tous; universelle de plein droit, délire partagé, il suffit de s’y tenir pour [162] n’être plus personne, anonymement dispersé dans la hiérarchie des ordres.

La science est le Dehors sans point de cécité.¹⁸

Réciproquement, la structure signifiante définie par la suturation sera désignée dans sa particularité (elle place le manque), et d’abord comme non-science. La suture ainsi n’est pas un concept du signifiant en général, mais la propriété caractéristique de l’ordre signifiant où vient se barrer un sujet. Nommément, l’idéologie.

Il y a toujours un sujet de l’idéologie, car telle est la marque marne à quoi elle se reconnaît. Place du manque, refente du fermé: concepts à partir de quoi construire la loi de fonctionnement du discours idéologique.

Qu’on mesure ce qui est ici en question: l’articulation possible du Matérialisme historique et de la Psychanalyse, le premier produisant la Topique d’ordres signifiants particuliers (les idéologies), la seconde les structures de leur efficace, les lois d’entrée et de connexion par quoi les places que l’idéologie distribue sont finalement occupées.

Si le Matérialisme historique prétend à lui seul élucider l’asservissement subjectif aux idéologies; ou si la psychanalyse efface dans la généralité d’une logique du signifiant la spécificité du lieu où elle doit repérer la marque du manque; alors ces disciplines sont pliées l’une à l’autre, rabattues l’une sur l’autre. Non stratifiées: non scientifiques.

Il importe donc d’affirmer que de la science la psychanalyse n’a rien à dire, si même des scientifiques, qui y sont asservis, elle peut beaucoup nous apprendre. Par ce silence, elle détermine négativement le signifiant dont elle parle et où elle articule le Désir. Le matérialisme historique redouble positivement cette détermination en produisant la configuration structurale où prend place l’instance idéologique.

Dès lors, poser que la différence science/idéologie puisse être effacée dans une logique de l’itération oscillante, et nommer un sujet de la science, c’est interdire que puissent se conjoindre, dans leur disjonction même, Marx et Freud.

Exhiber le concept de suture en l’endroit même de son inadéquation (la mathématique); et, mettant à profit le rabattement, par les savants, de la représentation (idéologique) de ce qu’ils font sur ce qu’ils font (une science), conclure à la légitimité de ce concept pour l’universel des discours, c’est réfléchir la science dans l’idéologie: la déstratifier pour lui prescrire son manque.

[163]

Appelons ‘philosophie’ la région idéologique spécialisée dans la science: chargée d’effacer la coupure en montrant le signifiant scientifique comme paradigme régional du signifiant-en-soi: rapport de Platon à Eudoxe, de Leibniz à Leibniz, de Kant à Newton, de Husserl à Bolzano et Frege; peut-être de Lacan à la Logique mathématique.

La science, nous l’avons indiqué, est ce qui n’est rapporté qu’à soi, le dehors multiple. Aucun ordre signifiant ne peut envelopper les strates de son discours.

De là l’impossibilité récurrente de la philosophie, dont l’historicité polymorphe atteste qu’en elle joue bien la loi de l’idéologie: la philosophie véhicule et insiste la marque de son manque.

Et que lui manque-t-il? L’effacement de la coupure suppose la construction intra-philosophique d’un concept de la science. La philosophie est astreinte à marquer, dans son ordre propre, le signifiant scientifique comme espace total. Mais la science, indéfiniment stratifiée, forclusion multiple, différence de différences, ne peut recevoir cette marque. La multiplicité de ses ordres est irréductible¹⁹: ce qui, dans la philosophie, s’énonce comme science, est inévitablement le manque de la science. Ce dont la philosophie manque, et à quoi elle se suture, est son objet même (la science), en elle cependant marqué par la place qu’il n’y occupera jamais.

C’est en toute rigueur qu’il est possible d’avancer que la science est le Sujet de la philosophie, et ce précisément parce qu’il n’y a pas de Sujet de la science.

Soit à dire, reprenant l’invocation de Leibniz: pour que l’idéologie soit sauve (comprenons: la classe dominante), doit y être placée l’infermable ouverture qu’y déchire la science. La philosophie s’accomplit dans ce placement.

C’est pourquoi la science et la pratique de la science mettront toujours la philosophie au supplice. Convoquant le multiple à son auto-suffisance, le jeu scientifique nous réjouit par l’enseignement de sa non-présence (sinon sous les espèces de ce qu’y induit son manque) dans le discours philosophique. Par la science nous apprenons qu’il y a du non-suturé, du forclos où le manque même ne manque pas, et qu’à nous déployer le contraire, sous la figure de l’Être qui se ronge, et que hante la marque du non-être, la philosophie s’épuise à maintenir en vie sa production suprême et particulière: Dieu ou l’Homme, selon les cas.

Spinoza l’avait catégoriquement affirmé.²⁰ Tout aussi bien Lautréamont, [164] prononçant avec quelque gourmandise sacrée l’éloge des mathématiques:

“O mathématiques sévères, je ne vous ai pas oubliées, depuis que vos savantes leçons, plus douces que le miel, filtrèrent dans mon cœur, comme une onde rafraîchissante” (Maldoror, ‘Chant deuxième’).

Car Lautréamont, livrant la clef de son enthousiasme, ajoute superbement: “Sans vous, dans ma lutte contre l’homme, j’aurais peut-être été vaincu.”

Dans les mathématiques en effet, rien ne manque qui ne soit déjà signifiant: marques substituées indéfiniment à elles-mêmes dans la complication de leur errance enchevêtrée.

La science est le véritable archi-théâtre de l’écriture: traces, traces biffées, traces de traces; mouvement où jamais nous ne nous exposons à rencontrer cette détestable figure de l’Homme: le signe du rien.

Janvier 1967

Appendice: Le théorème de Gödel et la chaîne d’alternance science-idéologie

Au regard de quelles tentatives le théorème de Gödel peut-il être assigné comme limitation? Deux, essentiellement.

I) Celle - métaphysique - qui, par Hilbert, enjoint au système formel de se fermer sur l’énoncé intérieur de sa propre cohérence.

La mathématique, soumise à cette ordonnance, n’exposerait plus le savoir à la béance indéfinie où elle étage ses ordres signifiants: sous les espèces, comme dit Husserl, d’un système nomologique, elle proposerait aux maléfices constituants de la philosophie un langage clos, unique, auto-normé, et venant, de lui-même immobile, effacer la blessure qu’ouvre historiquement dans la trame idéologique le fait de la science.

Contraindre le signifiant scientifique à occuper de son propre aveu la place où s’occulter, assez joli tour, auquel, cependant, ce signifiant se dérobe. On verra pourquoi.

II) Celle qui prétend épuiser, dans la reconstruction intégralement maîtrisée d’un système logistique, ce qui d’ailleurs se présente selon l’opacité résultante d’une histoire: disons l’arithmétique ‘intuitive’ .

De la première exigence, nous avons dit ce qu’il fallait penser. Elle illustre admirablement l’échec de la philosophie à prescrire aux écritures de la mathématique fût-ce l’unité d’un espace d existence. Elle éprouve la résistance de la stratification aux schèmes de fermeture que, pour son propre salut, la philosophie tente de lui imposer.

[165]

Ainsi des pythagoriciens, architectes métaphysiques du Nombre, pour qui la diagonale du carré représenta en son temps la limitation: limitation corrélative d’une attente qu’ordonnait la position du nombre entier dans l’illimité opératoire d’un Principe. C’est cette illimitation principielle dont le déjeté de l’irrationnel, fixant la différence d’une autre strate, attesta la signification extra-mathématique: idéologique.

Occasion d’affirmer qu’il n’y a pas, qu’il ne peut y avoir de crise dans la science, car la science est l’affirmation pure de la différence.

Qu’en revanche une crise dans la représentation (idéologique) de la science puisse induire un remaniement (positif) de la science même, ne saurait surprendre, puisque le matériau de la science est, en dernière instance, l’idéologie, et qu’une science ‘a priori’ se définit de n’avoir affaire, dans l’idéologie, qu’à ce qui l’y représente: science se coupant incessamment de sa propre indication dans l’espace représentatif.

Reste à parler du ‘hiatus’ qu’on repérerait entre Formalisme et Intuition, le premier échouant à dériver tout le vrai de la seconde.

Notons d’abord que l’intuitif considéré doit être défini comme l’état historique d’une science, dans l’enchevêtrement reçu, habité, de son épaisseur; la circulation licite, adhérente, de ses écritures.

Le problème rapporte donc un artifice scriptural entièrement codé à l’immanence d’un discours historico-institutionnel, qui vit de ce que l’exercice et le temps y autorisent des abréviations, des demi-mots, et le ponçage univoque d’une masse inoffensive de signifiants ‘normaux’ .

Notons aussi que le paradoxe dont use implicitement Gödel est présent dans le langage ordinaire sous l’antique enseigne du Menteur: énoncé qui s’épuise à énoncer sa propre fausseté.

Aussi bien la ‘limitation’ revient à la possibilité de construire, dans un langage formel, un prédicat de la non-dérivabilité (soit ~ D) et à appliquer ce prédicat à un représentant de l’énoncé formé par cette application même. Soit ~ D(n) où n, en un sens qui fait la preuve, ‘représente’ ~ D(n).

Le théorème de Gödel exprime donc, bien plutôt qu’un hiatus, la reprise, dans la transparence architectonique du système, de quelques ambiguïtés produites dans le langage par le concept (idéologique) de Vérité. Le Dérivable, si on prétend lui faire subsumer le Vrai, fonctionne comme ce dernier en chausse-trappe à la jointure insaisissable de la science et de son dehors.

Théorème, donc, de fidélité du formalisme aux stratifications et connexités qui sont à l’oeuvre dans l’histoire des sciences, pour autant qu’elles en expulsent tout usage principiel (illimité) du Vrai.

Encore faut-il, pour le savoir, s’y exercer. Nous allons donner à cette fin une démonstration largement intuitive, mais complète et rigoureuse, du noyau significatif d’un théorème de limitation.

Cette démonstration est empruntée à R. M. Smullyan, Theory of Formal Systems, Princeton, 1961.

La préoccupation pédagogique domine notre exposé: en principe, la preuve ne requiert aucune connaissance mathématique particulière, ce qui ne veut pas dire qu’on puisse la lire distraitement.

L’exposé proprement dit est accompagné de commentaires entre parenthèses, qui sont, de cet exposé, le redoublement sémantique, et le plus souvent dangereusement idéologique. Leur fonction est didactique.

[166]

Les rares notations accompagnées d’un !! ne sont pas nécessaires à l’intelligence de la déduction, mais la suturent au discours des lecteurs qui, sachant un minimum de mathématiques, seraient tentés légitimement d’anticiper sur ma lenteur.

Voici la structure de la démonstration:

I. Description du système.

1) mécanisme-2;

2) numérotation des écritures produites par le M₂ (fonction g);

3) fonction de représentation (fonction φ);

4) mécanisme-3;

5) consistance.

II. Lemme de diagonalisation.

1) diagonalisation et classes W*;

2) énoncés de Gödel;

3) représentation d’une classe de nombres par un prédicat;

4) lemme de diagonalisation,

III. Condition d’existence d’un énoncé indécidable.

(Dans la suite, le rappel d’un résultat se fera selon ce tableau: si par exemple on évoque la condition de consistance, on notera: (I, 5).)

I. Description du système.

1. Mécanisme-2.

Désignons par E la production d’un mécanisme-2 (d’une syntaxe), soit l’ensemble des expressions bien formées d’un système logique.

Nous supposerons que figurent dans cette production, parmi d’autres écritures:

- Des prédicats p, dont l’ensemble sera appelé P.

- Des énoncés fermés, dont l’ensemble sera appelé S.

(Remarquons dès à présent que ces appellations concernent la lisibilité sémantique de la démonstration. On pourrait se contenter des données purement ensemblistes; E, P ⊂ E, S ⊂ E.)

2. Numérotation des expressions.

Nous allons maintenant nous donner l’ensemble des nombres entiers, soit N, dans son acception ‘intuitive’ : tel qu’y peut circuler tout héritier de la tradition arithmétique: 1, 2, 3, et le reste.

Et nous allons supposer que nous avons numéroté toutes les expressions de E. Autrement dit, qu’à toute écriture e ∈ E, correspond un nombre entier, noté g(e); nous supposons en outre qu’inversement tout nombre entier est le correspondant d’une expression de E, et d’une seule.

!! Nous posons donc l’existence d’une application bi-univoque g de E sur N.

(Cette étape est essentielle; elle inscrit les écritures de M₂ comme infini dénombrable. Si en outre notre système ‘formalise’ l’arithmétique, il pourra ‘parler’ de ses propres écritures, en ‘parlant’ des nombres qui correspondent el ces écritures par la fonction de numérotation.)

[167]

3. Fonction de représentation

(Nous voulons maintenant donner sens à l’idée que notre système est fort : qu’il opère sur les écritures de l’arithmétique.

Intuitivement - et vaguement -, cela peut signifier que l’écriture formée par une expression et un nombre est une expression nouvelle, intérieure au système. Si l’on veut: qu’en ‘appliquant’ une expression à un nombre, on obtient une écriture du système, qui ainsi se trouve ‘parler’ des nombres.)

Nous allons considérer qu’il existe une fonction φ, dite fonction de représentation, qui associe au couple formé par une expression et un nombre entier, une autre expression. Soit:

φ(e, n) = e′

(avec e ∈ E, n ∈ N, e′ ∈ E).

!! φ est donc une application de E × N dans E. On a:

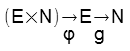
(Le cas le plus intéressant est celui où expression e est un prédicat: intuitivement, φ(p, n) peut ‘exprimer’ l’application au nombre n de la ‘propriété’ p. Et on doit alors pouvoir se demander, sans ambiguïté, si l’expression φ(p, n) est vraie ou non; si le nombre n a, ou non, cette propriété. Il faut donc pouvoir considérer l’expression φ(p, n) comme complète, produisant un sens justifiable univoquement d’une évaluation.)

Nous poserons que toute expression φ(p, n) est un énoncé fermé (appartient à S. Voir I, I): φ(p, n) ∈ S.

4. Mécanisme-3

Qu’un mécanisme-3 (de dérivation, de démonstration) opère sur les énoncés fermés veut dire:

- Qu’il existe dans S un ensemble d’expressions dites démontrables. Soit D cet ensemble (D ⊂ S).

(S - D) représente, alors, l’ensemble des énoncés non-démontrables,

- Qu’il existe aussi dans S un ensemble d’expressions réfutables, soit R. (R est donc l’ensemble des expressions dont la négation est démontrable.) (R ⊂ S).

(Nous faisons bien apparaître les deux conditions qui caractérisent un mécanisme-3; la dichotomie (dérivable et non-dérivable, D etS - D): la correspondance par négation, qui regroupe les expressions dont on peut dériver la négation (R).

Le problème de Gödel est alors de savoir si tout énoncé (fermé) non-démontrable est réfutable. Peut-on toujours poser: (S - D) = R?

Notre propos est d’établir des conditions de structure qui rendent impossible cette égalité.)

[168]

5. Consistance.

Nous souhaitons qu’il ne puisse pas y avoir d’empiétement du démontrable sur le réfutable, ce qui équivaudrait à une contradiction. Aucune expression ne doit donc appartenir simultanément à D et à R: le système sera dit consistant si l’intersection de ces deux ensembles d’expressions est vide: D ∩ S = Ø.

!! Au niveau de généralité où nous nous tenons, il est évidemment possible de se passer de toute interprétation, et de dire qu’on se donne:

- E, P ⊂ E, S ⊂ E, R ⊂ S, D ⊂ S.

- R ∩ D = Ø.

- N, E → N (g biunivoque sur).

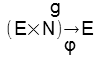, avec (∀p)(∀n)[(p ∈ P, n ∈ N) → φ(p, n) ∈S].

II. Lemme de diagonalisation

1. Diagonalisation et classes W *.

Parmi les expressions du type φ(e, n), il en est de très intéressantes: celles où le nombre n est précisément le nombre g(e) qui ‘numérote’ (voir I, 2) l’expression e.

L’expression φ(e, g(e)) est appelée la diagonalisation de e.

(Nerf de la preuve: on ‘applique’ l’expression au nombre qui la ‘représente’ .)

Considérons maintenant un ensemble d’expressions de E, absolument quelconque, soit W (on a simplement W ∈ E).

Supposons que figurent, dans W, des expressions diagonales, du type φ(e, g(e)). Nous allons associer, à l’ensemble d’expressions W, la classe de nombres W*; cette classe W* comprendra tous les nombres qui numérotent des expressions dont la diagonalisation est dans W.

Appartenir à W*, pour un nombre n, signifie qu’il existe une expression e telle que:

a) g(e) = n(n ‘représente’ e)

b) φ(e, g(e)) ∈ (la diagonalisation de e est dans W).

Ou encore, en employant le classique symbole ↔ pour l’équivalence:

n ∈ W* ↔ [n = g(e)] et [φ(e, g(e)) ∈ W]

Naturellement, si W ne contient aucune expression diagonale, W* est la classe vide.

[169]

On a donc la situation suivante:

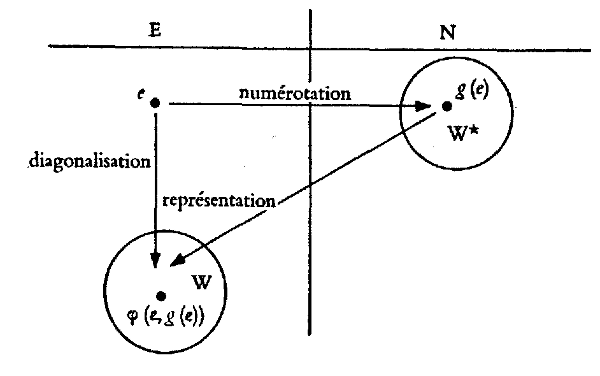
!! Soit φd la fonction-diagonale définie sur E par: φd(e) = φ(e, g(e)).

On a: W* = g º φ_d^-1 (W).

2. Énoncé de Gödel pour un ensemble d’expressions

L’idée directrice est maintenant d’associer à un ensemble W d’expressions un énoncé (fermé) tel que sa ‘vérité’ dépende de sa position par rapport à W. Autrement dit un énoncé qui est démontrable si et seulement si il appartient à W.

Un tel énoncé (appartenant à S, voir I, 1), soit G, satisfait donc (rappelons que D est l’ensemble des énoncés démontrables):

G ∈ D ↔ G ∈ W

On l’appelle un énoncé de Gödel pour W.

(Un énoncé de Gödel pour l’ensemble d’expressions W, s’il existe, est donc un énoncé dont la démontrabilité est ‘exprimable’ en termes d’appartenance à W. Nous avons ici une sorte d’équivalent de ce que Gödel démontre - laborieusement - dans son système; qu’on y peut construire le prédicat: ‘démontrable dans le système’ .)

3. Représentation d’une classe de nombres dans le système

On dira qu’un prédicat p∈ P (voir I, 1) représente une classe de nombres entiers A ⊂ N, si l’on a:

φ(p, n) ∈ D ↔ n ∈ A

( ‘L’application’ de p au nombre n donne un énoncé démontrable si et seulement si ce nombre appartient à la classe A. Il s’agit là d’une élaboration très formelle de l’idée intuitive suivante; la propriété p n’appartient qu’aux nombres de la classe A. Ou: la classe A est l’extension du concept p.)

[170]

4. Lemme de diagonalisation

Nous allons démontrer la proposition suivante:

Si la classe de nombres entiers W* est représentable dans le système par un prédicat, alors il existe un énoncé de Gödel pour l’ensemble d’expressions W.

Soit p le prédicat qui représente W*. Par définition (paragraphe précédent):

φ(p, n) ∈ D ↔ n ∈ W*

En particulier, pour n = g(p)

i) φ(p, g(p)) ∈ D ↔ φ(p, g(p)) ∈ W*.

(La diagonalisation du prédicat p est démontrable si et seulement si la numérotation de p appartient à W*.)

Mais (voir II, 1), la définition même de la classe W* est:

ii) g(p) ∈ W* ↔ φ(p, g(p)) ∈ W.

En confrontant les équivalences (i) et (ii), nous obtenons (par substitution d’un terme équivalent à celui de droite dans (i); ou, si l’on veut, en appliquant la transitivité de l’équivalence):

φ(p, g(p)) ∈ D ↔ φ(p, g(p)) ∈ W.

Nous reconnaissons (II, 2) la définition d’un énoncé de Gödel pour W: φ(p, g(p)) est cet énoncé (c’est bien en effet un énoncé fermé, puisque - (voir I, 3) - nous avons posé que pour un prédicat l’expression φ(p, n) appartient toujours à S).

(Qu’avons-nous démontré? Que si une classe W* (de nombres) est représentée par un prédicat dans le système, la diagonalisation de ce prédicat est un énoncé de Gödel pour l’ensemble d’expressions W.

Faisons un pas de plus dans la description (idéologique) de ce résultat.

Soit un ensemble quelconque d’expressions, W. Supposons que W contienne des expressions diagonales (expressions ‘appliquées’ au nombre qui les représente dans la numérotation des expressions), On considère alors l’ensemble des nombres qui numérotent ces expressions diagonales. Cet ensemble est W* (voir schéma dans II, 1).

Dire que W* est représenté dans le système, c’est dire qu’il existe un prédicat dont le ‘sens’ est: ‘être un nombre qui représente une expression diagonale contenue dans W.’

Diagonalisons ce prédicat ( ‘appliquons’ le à son propre représentant numérique). Nous obtenons un énoncé dont le sens serait quelque chose comme;

“Le nombre qui représente le prédicat ‘être-un-nombre-qui-représente-une-expression-diagonale-contenue-dans-W’ est lui-même un nombre qui représente une expression diagonale contenue dans W”.

C’est cet énoncé qui n’est démontrable que s’il appartient à W; c’est donc un énoncé de Gödel pour W.

On y reconnaîtra la structure sous-jacente aux procédés diagonaux qui, depuis Cantor, ont donné son principal instrument à la mathématique ‘fondamentale’ : construire un énoncé qui affirme de lui-même son appartenance à un groupe d’expressions que par ailleurs cet énoncé représente ou désigne.)

[171]

III. Condition d’existence d’un énoncé indécidable.

L’idée directrice, qui va compléter l’argument, est fort simple: Nous allons appliquer le lemme de diagonalisation à la classe R des énoncés réfutables. Et nous obtiendrons ainsi très facilement le théorème de Gödel: si R* est représentable (au sens de II, 3, il existe un énoncé qui n’est ni démontrable, ni réfutable. (Qui n’appartient ni à D, ni a R.)

Si R* est représentable, il existe un énoncé de Gödel pour R (lemme de diagonalisation). Soit G cet énoncé. Par définition (II, 2):

G ∈ D ↔ G ∈ R

(G est démontrable si et seulement si il est réfutable ...)

Mais D ∩ R = Ø

(D et R n’ont aucun élément commun: hypothèse de consistance, I, 5.)

G n’appartient donc ni à D ni à R: c’est un énoncé indécidable.

(Que signifie l’hypothèse initiale: R* est représentable? Elle signifie qu’il existe dans le système un prédicat dont le ‘sens’ serait: ‘être un nombre qui représente une expression diagonale réfutable’ .

Quant à l’énoncé de Gödel pour R - l’énoncé indécidable - nous savons, par la démonstration du lemme, qu’il n est autre que la diagonalisation du prédicat qui représente R*. C’est donc un énoncé dont le ‘sens’ serait quelque chose comme:

“Le nombre qui représente le prédicat ‘être-une-expression-diagonale-réfutable’ représente lui-même une expression diagonale réfutable.”

On reconnaîtra la parenté avec l’argument ‘intuitif’ du Menteur.)

Cette démonstration met en évidence le noyau de la découverte de Gödel: si l’on peut construire dans un système un prédicat de la réfutabilité, son ‘application’ aux expressions diagonales donne lieu à l’indécidabilité d’une certaine classe d’énoncés.

Cette démonstration met également en lumière le cheminement en zig-zag qui organise la preuve ‘entre’ le système formel et la théorie ‘intuitive’ des entiers: c’est la représentation (numérotation) des expressions qui permet la diagonalisation. Inversement, c’est la construction dans N des classes W* qui, ‘reprise’ prédicativement dans le système, permet la démonstration cruciale du lemme. Dans notre langage, nous dirons que la preuve opère ici sur des connexités de strates, qui autorisent des parcours et des correspondances.

La complication scrupuleuse de la démonstration de Gödel, par rapport à celle de Smullyan, tient à ce que le premier doit établir pour un système déterminé (en gros, celui des Principia Mathematica) la représentabilité de R*.

Mais le point de vue très général adopté par Smullyan dégage clairement le caractère positif et structural de la découverte: comme très souvent en mathématiques, elle développe un réseau de contraintes conditionnelles: si l’on prescrit à notre système la consistance (D ∩ R = Ø) et une capacité représentative [172] ‘forte’ (la classe de nombres R* est ‘désignée’ par une expression de E), on peut construire un ‘reste’ dans l’ensemble des énoncés: montrer que les ensembles disjoints D et R ne forment pas un recouvrement de S.

Prenons garde que les concepts de représentabilité, de consistance, de disjonction, de numérotation etc., sont ici mathématiquement assignés, et ne conservent rien de leurs connotations empiriques ou philosophiques. Le concept de ‘représentant’ en particulier, nous ne l’avons utilisé que pour faire image, en lieu et place de ce qu’il recouvre: des fonctions (g et φ), définies de la façon la plus classique.

Le résultat de Gödel n’est donc particulier, dramatique, qu’au regard d’une saturation sémantique qui rabat sur le discours de la science une attente idéologique.

Qui pose à la logique des questions qui ne sont pas des problèmes, s’expose à ressentir comme résistance ce qui n’est que le déploiement des contraintes régionales où advient l’objet factice de cette science.

Ainsi retrouvons-nous la dialectique articulée de la science et de l’idéologie. Pour le problème qui nous intéresse, les étapes en sont les suivantes:

I. Existence d’une mathématique historique (soit: l’arithmétique ‘intuitive’ ), principiellement ouverte (signifiant indéfiniment stratifie).

IIa. Re-présentation idéologique de cette existence comme norme transmathématique de la rationalité intégralement maîtrisable (déstratification idéologique du signifiant mathématique).

IIb. Question posée aux mathématiques de leur conformité à la norme idéologique: intention axiomatique et formaliste, visant à exhiber une transparence fondée. (Motivations idéologiques de Frege et Russell.)

III. Coupure: traitement mathématique de la re-présentation idéologique des mathématiques: Construction effective de systèmes formels ‘représentant’ l’arithmétique historique (Principia Mathematica)

IVa. Re-présentation idéologique de la coupure: les systèmes formels, conçus comme normes trans-mathématiques de la fermeture rationnelle. Idée d’un système nomologique (Husserl).

IVb. Question posée aux mathématiques de leur conformité absolue à la norme idéologique de fermeture. Intention méta-mathématique, relative à la démonstration intérieure de la consistance d’un système (Hilbert).

V. Coupure: traitement mathématique de la re-présentation idéologique. Construction effective d’une méta-mathématique mathématique (arithmétisation de la syntaxe).

Théorème de Gödel: la stratification structurale du signifiant mathématique ne répond pas à la ‘question’ de la fermeture.

VI. Re-présentation idéologique de la coupure: au regard de l’attente normative, le théorème de Gödel est vécu comme limitation.

Exégèse idéologique de cette limitation, comme:

- parole ouverte et recel de l’être (Ladrière);

- finitude;

- refente, suture;

- …

VII. Coupure: théorie générale de l’effet-limitation, conçu positivement comme instance structurale de certains objets mathématiques (vérité épistémologique de Smullyan).

[173]

L’enseignement épistémologique de cette aventure croisée nous rappelle que la mathématique opère sur sa propre existence en tant qu’indiquée dans l’idéologie, mais que cette opération, conforme aux contraintes spécifiques d’une science, prend la forme d’une coupure; en sorte que les questions (idéologiques) dont, à titre de matériau, la mathématique opère la reprise oeuvrante, ne trouvent en elle aucune réponse.

A venir figurer dans l’espace problématique des mathématiques, une image idéologique de cette science ne peut qu’être désormais méconnue par celui qui la prodiguait. Car de matériau devenue produit, elle se conforme à des règles d’existence que rien, dans le matériau, ne pouvait indiquer.

Où l’on voit en toute rigueur que la science est science de l’idéologie, et même science de l’idéologie de la science de l’idéologie, aussi loin qu’on voudra. Mais l’idéologie ne s’y retrouve jamais.

Telle est la loi de chaîne alternée où insiste ce qu’on nomme ‘progrès de la science’ : ce n’est pas parce qu’elle est ‘ouverte’ que la science a motif à se déployer (bien que l’ouverture règle la possibilité de ce déploiement): c’est parce que, de cette ouverture, l’idéologie est inapte à se satisfaire. Forgeant l’impraticable image du discours fermé, enjoignant à la science de s’y plier, elle se voit renvoyer son ordre méconnaissable sous les espèces du concept nouveau, du remaniement par quoi la science, traitant comme matériau l’interpellation idéologique, déplace incessamment la brèche qu’elle y ouvre.

Mesurons ici - cette fois au plus près de Lacan - le ridicule des motivations du progrès par ‘l’intention’ de découverte.

Du théorème de Gödel, et de la connotation limitative où, après les irrationnels, les négatif et les imaginaires, il s’est annoncé, retenons que la science avance précisément par ceux qui, lui posant la question de son arrêt, ordonnent désespérément le lieu où reconnaître que cette question, pour reprise qu’elle soit, n’est pas même entendue.

Janvier 1967.

Notes

1. Cf. Frege, ‘On sense and nominatum’, in Readings in Philosophical Analysis, Feigl et Sellars, N.Y. 1949. (p. 85-102).

“Tout énoncé assertif, à quelque domaine qu’appartiennent les dénotations des mots qui y figurent, doit donc être tenu pour un nom propre; et sa dénotation, si elle existe, est soit le Vrai, soit le Faux.”

“Tous les énoncés vrais ont ainsi le même dénotation.” ↵

2. Par logique du Signifiant, nous entendons ici le système des concepts par lesquels penser l’articulation du sujet: Manque, Place, Tenant-Lieu, Suture, Forclusion, Refente. Ces concepts ont été produits par J. Lacan, et c’est reconnaître à son égard une dette définitive que d’engager le procès de limitation de leur usage: le procès critique.

La thèse que nous soutenons va seulement à esquisser l’impossibilité d’une logique du Signifiant enveloppante au regard de l’ordre scientifique, et où s’articulerait l’effacement de la coupure épistémologique. ↵

3. L’opérateur privilégié de cette dissimulation est le concept de sens, à quoi l’on rapporte et l’origination du Vrai (dérivabilité) et le rejet du non-sens (formation-syntaxe). ↵

4. Que la division soit sans reste veut dire: étant donnée une écriture quelconque (une suite finie de signes de l’alphabet), il existe un procédé effectif qui permet de déterminer sans ambiguïté la conformité ou la non-conformité de l’expression aux règles de la syntaxe.

Pour les logiques classiques, cette propriété syntaxique fait l’objet d’une démonstration par récurrence portant sur le nombre de parenthèses de l’expression.

Cf. S. Kleene, Introduction to Metamathematics, Amsterdam, 1964, p. 72 s ↵

5. Une machine forte est capable de répartir les écritures de l’arithmétique récursive.

Notons qu’il existe un mécanisme logique faible, mais parfait: le Calcul des Propositions. Ce système est en effet:

– Consistant à tous les sens du terme,

– Décidable (de toute expression bien formée, on peut savoir mécaniquement si elle est ou non dérivable),

– Complet (toute expression bien formée est, ou dérivable, ou telle qu’ajoutée aux axiomes elle rend le calcul inconsistant),

– Catégorique (tous les modèles sont isomorphes).

La seule existence de ce Calcul pose quelques problèmes à la Logique du Signifiant, car rien, fût-ce une place vide, n’y atteste un manque. Très rigoureusement, ce système ne manque de rien, ni ne marque le rien dont c’est même déjà trop dire qu’il en manque.

On peut soutenir que la perfection du Calcul des Propositions est le référent différentiel intra-logique de ‘l’imperfection’ relative des autres systèmes. ↵

6. C’est une question différente de déterminer si, pour toute expression bien formée, il existe un procédé mécanique (effectif) permettant de savoir ‘d’avance’ (sans avoir à la dériver) si elle est, ou non, dérivable.

L’existence d’un tel procédé définit la décidabilité du système. On sait (Church, Kleene) que les mécanismes logiques assez forts sont généralement indécidables.

On ne confondra pas la décidabilité d’un système avec l’existence ou la non-existence d’un énoncé tel que ni lui ni sa négation ne sont dérivables. Le problème de l’existence d’un énoncé indécidable n’est pas un problème de décidabilité, mais un problème de complétude.

Un système peut être décidable et incomplet: il y existe alors des énoncés (indécidables) dont on peut ‘décider’ à l’avance, par un procédé effectif; qu’ils ne sont ni dérivables ni réfutables. La réciproque cependant n’est pas vraie: un théorème méta-mathématique important lie les résultats d’indécidabilité (Church) aux résultats d’incomplétude (Gödel). Si un système formel (assez fort) est indécidable, alors il est ou inconsistant, ou incomplet. ↵

7. Conformément à l’usage, nous noterons ~, dans tout le reste de cet exposé, le foncteur de négation. ↵

8. Quant à y déchiffrer le hiatus entre l’intuition et le formalisme, nous ne nous y risquerons pas. Sur ce point, voir notre appendice sur la démonstration de Smullyan, et notre critique du concept de limitation. ↵

9. ‘Idéalement’ puisque, s’il est vrai que toute expression bien formée est dans T ou dans NT, l’existence d’un procédé ‘effectif’ (récursif algorithmique) permettant de déterminer dans laquelle de ces deux classes elle figure, est souvent démontrée impossible. C’est le problème de la décidabilité du système (cf. note 6). ↵

10. Cf. ‘La Suture’, in Cahiers pour l’analyse, no. 1. ↵

11. Church a selon nous raison d’identifier en dernière instance la Sémantique et le Syntaxe (Cf. Introduction to Mathematical Logic, Princeton 1956, p. 65: “L’assignation de dénotations et de valeurs aux expressions bien formées peut consister en correspondances abstraites; leur traitement appartient alors à la syntaxe théorique.”)

La Sémantique ne devient logique (scientifique) que si elle est la syntaxe de la différence des syntaxes. ↵

12. Activité rationaliste de la Physique contemporaine, p. 5. ↵

13. Dans un calcul du deuxième ordre, où l’on peut quantifier les prédicats, l’égalité serait définie explicitement, selon l’instance leibnizienne des indiscernables, ici restreinte à l’ordre des signes: deux variables d’individu qui tombent, sans exception, sous les mêmes prédicats, sont partout substituables, rien ne marquant leur différence. Avec les notations classiques:

I(x, y) = _df (∀a) [a(x) ⊃ a(y)] ↵

14. Nous noterons désormais M₁, M₂ et M₃ les mécanismes de concaténation, de syntaxe (du calcul des prédicats) et dérivation (idem). ↵

15. On s’étonnera peut-être de ce que nous construisions ici le zéro, non comme un terme, mais comme un prédicat.

Mais c’est à J. A. Miller qu’il faut poser la question relative à la reprise qu’il fait de l’indistinction où Frege maintient variables d’individu et variables prédicatives. Pour Frege, certes, un prédicat est un terme. Mais cette position est intenable, car elle donne lieu au paradoxe de Russell, qui devait précisément ruiner l’arithmétique formelle de Frege.

Or, le texte de Miller n’intègre pas à son usage métathéorique de la construction du nombre l’inconsistance théorique de cette construction. De là une incertitude épistémologique, dissipée seulement si on distingue, à chaque mention du texte (mêlé) de Frege, son niveau de fonctionnement. Soit:

a) Un effort théorique de construction des cardinaux finis.

b) Les erreurs théoriques dans cet effort (non-stratification des variables).

c) La re-présentation idéologique du théorique (dénotation, concept, nombre du concept, etc.).

d) La re-présentation idéologique des erreurs théoriques (théorie du zéro). ↵

16. Les calculs ramifiés (les diverses instances de la théorie des types) tentent le rabattement de la stratification sur une seule strate, la construction d’une logique de la stratification qui ‘exprimerait’ la stratification de la logique.

L’inévitable axiome de réductibilité désigne un certain échec de cette tentative (cf. par exemple W.V.O. Quine, ‘On the axiom of reducibility’ in Mind, 45, p. 498-500).

Le système ‘expansif’ Σ de Hao Wang est plutôt un parcours constructif de la stratification. Il n’en est pas moins exposé à de considérables difficultés relatives à la construction des ordinaux (Cf. par exemple Hao Wang, A Survey of Mathematical Logic. p. 559 s, surtout p. 643, Pekin, 1964).

Nous sommes pour notre part convaincu que la multiplicité stratifiée du signifiant scientifique, inhérente au procès de production de la science, est irréductible à un seul de ses ordres. L’espace des marques ne s’y laisse pas projeter sur un plan. Et ce n’est là une résistance (une limitation) qu’au regard d’un vouloir métaphysique. Le vouloir scientifique est la transformation-parcours de l’espace stratifié, non son rabattement. ↵

17. J. A. Miller, ‘L’action de la structure’, Cahiers pour l’Analyse, 9. ↵

18. Si l’on se propose d’exhiber l’écriture comme telle, et d’en absenter l’auteur; si l’on veut obéir à Mallarmé enjoignant à l’ouvre écrite d’avoir lieu sans sujet ni Sujet, il existe un moyen radical, séculaire, et exclusif de tout autre: l’entrée dans les écritures de la science, dont telle est justement la loi.

Lorsqu’en revanche une écriture littéraire délectable sans doute, mais surchargée à l’évidence des marques de tout ce qu’elle nie, nous arrive à l’enseigne de ce qui se tient tout seul dans le Dehors scriptural, nous savons d’avance (c’est là un problème décidable ...) qu’elle exhibe l’idéologie de la différence, et non son procès de réalité.

Les écrivains, s’ils répugnent à se convertir aux mathématiques, doivent s’en tenir dans leurs programmes à l’honorable principe de leurs productions: d’être l’idéologie montrée, et par là, quoique autonome, irréductiblement suturée. ↵

19. Ce qui ne veut évidemment pas dire que des ‘synthèses’ régionales, des transferts, des intrications, soient impossibles. L’histoire des sciences pense la connexité locale des strates, et la stratification de cette connexité.

La grandeur d’A. Comte n’en demeure pas moins d’avoir aperçu qu’en dépit des déplacements et intersections qui pouvaient s’y produire, la multiplicité et la hiérarchie dans l’ordre signifiant étaient des propriétés inhérentes au concept de la scientificité. ↵

20. Texte célèbre, Livre I, appendice. L’homme n’aurait jamais transgressé l’illusion s’il n’y avait eu ce fait surprenant: les mathématiques. ↵