Concept and Form:
The Cahiers pour l’Analyse
and Contemporary French Thought

This project is funded by an Arts and Humanities Research Council (AHRC) research grant and is supported by the Centre for Research in Modern European Philosophy (CRMEP) and Kingston University's Faculty of Arts and Social Sciences.

Formelle sans être formaliste: ainsi Lukasiewicz caractérise-t-il la logique d’Aristote, par opposition à celle des stoïciens.¹ Elle est formelle, parce que les expressions qui lui appartiennent en propre sont des lois syllogistiques, qui ne comportent aucun terme concret, mais seulement des ‘emplacements’ pour des termes de ce genre, emplacements marqués par des symboles littéraux. La tradition aristotélicienne a identifié l’idée selon laquelle la logique est un instrument (ὄργανον) de la philosophie, et non une de ses parties (μέρος), avec l’idée selon laquelle n’appartiennent à la logique que les lois exprimées à l’aide de variables, à l’exclusion de leurs applications, c’est-à-dire des expressions où des termes concrets sont substitués aux variables.² La notion de forme en référence à laquelle la logique aristotélicienne peut être dite formelle est donc la “notion philosophique fort abstraite [...] de la forme dans son opposition à la matière”.³ Lukasiewicz décrit ainsi les éléments caractéristiques de la forme syllogistique, définie comme ce qui reste quand on élimine la matière du syllogisme “A la forme du syllogisme appartiennent, outre le nombre et la disposition des variables, ce qu’on appelle les constantes logiques. Deux d’entre elles, les conjonctions ‘et’ et ‘si’ , sont des expressions auxiliaires et font partie, comme nous le verrons plus tard, d’un système logique qui est plus fondamental que celui d’Aristote [la logique propositionnelle]. Les quatre constantes qui restent, à savoir ‘appartenir à tout’ , ‘n’appartenir à aucun’ , ‘appartenir à quelque’ et ‘n’appartenir pas à quelque’ , sont caractéristiques de la logique aristotélicienne. Ces constantes représentent des relations entre termes universels.”⁴

[4]

Formelle en ce sens, la logique d’Aristote n’est cependant pas formaliste. Ce n’est toutefois pas parce qu’elle fait largement usage du langage naturel, et qu’elle ne connaît d’autres symboles que ceux dont elle se sert pour dénoter les variables de termes. L’adoption d’un symbolisme entièrement artificiel n’est en effet qu’un moyen de satisfaire l’exigence essentielle du formalisme, qui est, pour reprendre encore les termes de Lukasiewicz, la suivante: “Le formalisme requiert que la même pensée soit toujours exprimée au moyen d’une série de mots exactement la même, ordonnée d’une manière exactement la même. Quand une preuve est mise en forme d’après ce principe, nous sommes en mesure de contrôler sa validité sur la base de sa forme extérieure seulement, sans faire référence à la signification des termes employés dans la preuve.”⁵ Rien n’empêche en principe de faire du langage naturel un usage formaliste; mais ce serait au prix d’une ascèse constante, difficile et fort peu économique, puisqu’il faudrait faire abstraction de la signification des termes, et leur réinventer une grammaire qui ne serait nécessairement ni tout à fait la même ni tout à fait une autre que leur grammaire naturelle; l’entreprise s’apparenterait à celle de cet inventeur qui s’était donné tant de mal pour retirer au caoutchouc son élasticité. Aristote, lui, n’emploie pas le langage naturel avec un tel luxe de précautions. Visant toujours le signifié à travers le signifiant, il s’autorise constamment des substitutions qui paraissent intuitivement évidentes, parce que substitut et substitué “veulent dire la même chose”⁶ mais qui ne sont pas explicitement légitimées par des définitions et des règles ad hoc. L’exemple le plus net que l’on puisse en donner est précisément l’expression des relations a, e, i, et o: on sait qu’Aristote substitue librement les unes aux autres, par exemple, les expressions suivantes:

A appartient (ὑπάρχει) à tout B.

A est prédiqué (κατηγορεῖται) de tout B.

A se dit de (λέγεται) tout B.

A suit (ἀκολουθεῖ) tout B.

B est en A comme en un tout (ἐν ὅλῳ).

Tout B est A.

Cette multiplicité d’expressions interchangeables pour une même ‘constante logique’ montre que ce qui intéresse Aristote est le signifié unique qu’il vise à travers elles. Le maniement des diverses constantes reste guidé par leur sens naturel; Aristote ne cherche pas par principe à les définir [5] intégralement par une grammaire si explicitement et rigoureusement formulée qu’il suffise d’en appliquer ‘aveuglément’ les règles pour pouvoir manier correctement les signifiants des constantes. Sa logique n’est pas un calcul; la notion de forme en référence à laquelle elle peut n’être pas dite formaliste est la “notion concrète, visuelle [...] de la forme au sens géométrique, ou, du moins, topologique: des dessins sur une feuille, combinés selon certaines règles, et susceptibles d’être transformés en tels dessins nouveaux selon certaines autres règles.”⁷

Décrire les effets de cette formalité sans formalisme, ce serait sans doute reprendre l’examen de toute la syllogistique aristotélicienne. Je me propose ici d’en étudier une incidence particulière avec quelque détail: le problème que posent le sens et l’usage de la proposition particulière, notamment en rapport avec le rôle qu’elle joue dans les procédures par lesquelles est démontrée la non-concluance des couples de prémisses autres que ceux des modes syllogistiques valides. J’espère en effet montrer que les textes relatifs à ces questions manifestent une modification significative de l’attitude d’Aristote, et qu’ils permettent de saisir sur le vif le travail du logicien, d’abord victime des équivoques du langage naturel, prenant ensuite de ces équivoques une conscience progressive, sous la poussée interne des problèmes eux-mêmes, et parvenant enfin à les maîtriser. Au terme de cette évolution, la proposition particulière abandonne celles de ses connotations usuelles qui perturbent son maniement logique, et n’est plus définie que par sa place dans un système d’oppositions, avec toutes les conséquences que cela comporte.

La proposition particulière traditionnelle, on le sait, est une source de problèmes épineux.⁸ Ceux que soulève sa ‘portée existentielle’ sont bien connus; toutes les consécutions de l’universel au particulier (subalternation, conversion ‘partielle’ de l’universelle, mode Darapti) les mettent en vive lumière.⁹ Un autre problème, non moins connu des logiciens, est celui de l’ambiguïté du système de ses relations avec les trois autres propositions comportant même sujet et même prédicat.¹⁰ On peut présenter ce problème en faisant remarquer que, dans son usage naturel, la proposition particulière paraît être engagée dans trois relations qui sont incompatibles entre elles:

(a) Sa vérité est en relation de contradiction (ou alternative) avec celle de l’universelle de qualité opposée. En dépit du proverbe, chacun admet que [6] l’exception infirme la règle. Et l’usage commun emploie sans cesse les équivalences:¹¹

AaB ↔ ~AoB

AeB ↔ ~AiB

(b) Sa vérité parait impliquée par celle de l’universelle de même qualité, sa subalternante:

AaB → AiB

AeB → AoB

A vrai dire, l’usage commun adopte à l’égard de la subalternation une attitude hésitante. Supposons un interlocuteur X qui soit persuadé que tous les A sont B; si un interlocuteur Y émet devant lui l’opinion que quelques A sont B, X pourra, selon l’humeur et les circonstances, lui répondre, ou bien: “Vous avez raison, mon cher, et plus encore que vous ne pensez, puisqu’en réalité tous les A sont B”, ou bien: “Vous avez tort, mon ami: il ne faut pas dire que quelques A sont B, il faut dire que tous les A sont B.” Mais je suppose que dans le second cas, Y serait porté à répliquer: “Nous sommes donc d’accord; puisque vous admettez que tous les A sont B, vous m’accorderez, à plus forte raison, que quelques A sont B”.

(c) Sa vérité parait impliquer, et être impliquée par, celle de la particulière de qualité opposée; la proposition ‘Quelques A sont B’ est ordinairement utilisée dans des situations où la proposition ‘Quelques A ne sont pas B’ est également tenue pour vraie.¹² Je prend un exemple au hasard, dans un livre à portée de ma main: il est clair qu’en écrivant “Il y a quelques syllogismes où ce mot [sc. ἀνάγκη] est omis,¹³ Lukasiewicz veut faire entendre qu’il existe aussi quelques autres syllogismes où ce mot n’est pas omis”. L’usage commun admet donc aisément l’équivalence AiB ↔ AoB.

Or il est évident que l’on ne peut maintenir concurremment les trois relations (a), (b) et (c). Si elles étaient tenues toutes trois pour vraies, de AaB supposé vrai on pourrait déduire à la fois ~ AoB, par (a), et AoB, par (b) et (c), ce qui est contradictoire. Pour un usage logique non contradictoire de la particulière, il est donc nécessaire d’abandonner l’une au moins des trois relations (a), (b) et (c). On obtiendra ainsi trois ‘carrés des opposés’ , trois systèmes de relations théoriquement concevables.¹⁴

[7]

I. Si l’on abandonne la relation (c), c’est-à-dire l’équivalence des deux particulières, on obtient le ‘carré’ traditionnel. On conserve les relations (a), c’est-à-dire les contradictions a-o et e-i, et les relations (b), c’est-à-dire les subalternations a-i et e-o; mais les subcontraires i-o cessent de s’impliquer réciproquement pour devenir simplement compatibles (elles peuvent être toutes deux vraies, mais ne le doivent pas; elles doivent seulement ne pas être toutes deux fausses). Corrélativement, les deux universelles sont contraires entre elles: elles ne peuvent être vraies toutes deux, mais elles peuvent être toutes deux fausses. L’interprétation que doit ici recevoir la particulière est: “Quelque A au moins est B (n’étant pas exclu que tout A soit B)”; de même pour la négative. J’appellerai cette proposition particulière minimale, et je la noterai i₁ ou o₁. Le carré correspondant est bien connu:

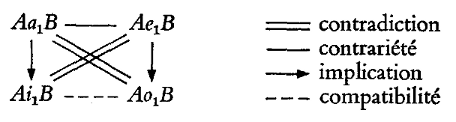
II. Si maintenant l’on abandonne les relations (b), en maintenant les relations (a) et (c), on obtient un système tout différent. Les deux particulières s’impliquent l’une l’autre; si l’on veut que les couples a-o et e-i restent contradictoires, on est conduit paradoxalement à admettre que chacune des particulières, d’une part exclut l’universelle de même qualité, et est exclue par elle, d’autre part continue à exclure l’universelle de qualité opposée et à être exclue par elle: en effet, chacune des universelles ne peut contredire une particulière sans contredire l’autre, qui lui est équivalente. Il suit en outre que les deux universelles sont maintenant équivalentes, puisqu’elles contredisent deux propositions équivalentes. Le carré devient alors le suivant:

[8]

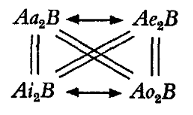
Ces paradoxes s’éclairent facilement si l’on donne de la particulière l’interprétation suivante: “Quelque A au moins et au plus est B” (que j’appellerai ici particulière maximale, en la notant i₂ ou o₂. Dans les termes du carré traditionnel, i₂ ou o₂ sont en effet tous deux équivalents à la conjonction i₁.o₂; et si l’on veut maintenir les contradictions entre a et o, i et e, a₂ ou e₂ se définiront toutes deux par la négation de cette conjonction, c’est-à-dire (en vertu des lois de dualité) par la disjonction ~ i₁ ∨ ~ o₁, en d’autres termes, a₁ ∨ e₁.¹⁵

III. On peut enfin imaginer, à titre récréatif, un système dans lequel on garderait les relations (b) et (c), en sacrifiant cette fois les relations de contradiction (a). Le maintien des implications a → i et e → o, et de l’équivalence i → o, imposerait alors d’admettre les implications a → o et e → i; le système ne comporte plus de contradictoires; si i et o sont des particulières, a et e ne peuvent plus être des universelles. La relation entre les postes a et e reste indéterminée: deux propositions qui en impliquent une même troisième (ici la conjonction i ⋅ o) ne sont liées par aucune relation nécessaire. Si, pour que le nouveau ‘carré’ d’opposition mérite encore ce nom, l’on choisit d’introduire entre a et e une relation de contradiction, on obtient cette conséquence supplémentaire, que les deux particulières sont toujours vraies: elles sont en effet impliquées par deux propositions dont il a été admis que l’une des deux est toujours vraie. Ce carré théorique aurait donc l’aspect suivant:

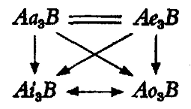
Il admet l’interprétation que voici: pour a et e, “un grand nombre de A sont (ne sont pas) B”; pour i et o, “un petit nombre au moins de A sont (sont pas) B”, étant entendu que toute relation universelle est exclue entre A et B.

Ce troisième système n’avait évidemment aucun titre à être retenu. Mais les deux autres en avaient l’un comme l’autre. Le premier a le mérite de la simplicité, mais il s’écarte de l’usage ordinaire en abandonnant l’équivalence des particulières; le second a les avantages et les inconvénients inverses.¹⁶

Aristote a opté sans l’ombre d’un doute, pour l’interprétation minimale de la particulière¹⁷; mais ce choix ne semble pas avoir été effectué d’emblée avec la pleine conscience de toutes ses exigences et implications; les connotations maximales de la particulière ‘naturelle’ ont exercé sur son travail une action perturbatrice. A cette absence de décision initiale, il a payé un lourd tribut de labeur et de complications, comme nous allons le voir maintenant.

La définition que donne Aristote de la particulière est contenue dans les lignes An. Pr. I.i, 24 a 18-20: “J’appelle universelle ‘la proposition énonçant que A’; appartient à tout ‘B’; ou n’appartient à aucun ‘B’; particulière ‘celle qui énonce que A’ appartient à quelque ‘B’; ou n’appartient pas à quelque ‘B’ ou n’appartient pas à tout ‘B’, indéfinie ‘celle qui énonce que A’ appartient ou n’appartient pas ‘à B’, sans ‘aucune note indiquant’ l’universalité ou la particularité.”¹⁸

A la prendre en sa lettre, la définition de la particulière affirmative est évidemment minimale. La présence de deux expressions distinctes pour la particulière négative (μὴ τινί - μὴ παντί) soulève cependant un problème: la conjonction ή qui les sépare a-t-elle la même valeur que celle qui les précède, c’est-à-dire celui de la disjonction exclusive aut? Rien n’empêche théoriquement de penser qu’Aristote distingue ici trois particulières: l’affirmative, [10] la négative minimale (μὴ τινί, en tant que simple négation de l’universelle, ne peut avoir que le sens minimal) et la négative maximale (μή τινί, à quoi il faudrait donner ce sens pour justifier sa disjonction d’avec μὴ παντί). Mais on peut écarter cette hypothèse, d’abord parce que si Aristote avait ici distingué o₁ et o₂ il aurait dû distinguer simultanément i₁ et i₂; ensuite parce que dans le cours de sa syllogistique, il ne reprend pas systématiquement la distinction μὴ παντί - μὴ τινί, et paraît traiter les deux expressions, dans les quelques passages où elles apparaissent, comme strictement équivalentes.¹⁹ Il faut donc considérer que dans la phrase définitionnelle, le ἤ qui sépare μὴ τινί et μὴ παντί a, contrairement à celui qui les précède, le sens d’un sive identificateur; la signification de μὴ τινί, qui reste peu claire, doit donc être déterminée comme étant la même que celle de μὴ παντί, qui est univoque et minimale.

Par ailleurs, il est bien connu qu’Aristote, s’il n’a pas tracé explicitement le traditionnel carré des opposés, n’en admet pas moins ses deux relations essentielles, les contradictions a-o et e-i, et les subalternations a-i et e-o.²⁰ Il repousse implicitement toute équivalence entre les subcontraires i et o dans l’analyse qu’il donne de leur relation: après avoir dit d’abord que c’est une relation de contrariété (ἐναντίως) au même titre que la relation a-e, et par opposition aux contradictions a-o et e-i, il précise ensuite que la contrariété i-o n’est pas une véritable opposition, sinon dans la forme verbale.²¹ Cela signifie qu’elles peuvent être vraies toutes deux, mais naturellement non qu’elles le doivent.

Il faut reconnaître toutefois que dans les exemples concrets qu’il donne de propositions particulières, Aristote utilise régulièrement des termes qui sont entre eux en relation d’appartenance particulière maximale, l’un des termes pouvant être inclus (homme-animal) ou non (blanc-animal) dans l’autre²²: homme convient à quelque animal, non à tous, blanc convient à quelque animal, non à tous. Il n’est cependant pas possible d’en tirer argument, comme le fait M. Sugihara, pour affirmer que la particulière aristotélicienne est maximale: ce serait en effet confondre la situation habituelle dans laquelle une proposition est utilisée avec la signification de cette proposition²³, les exemples capables d’illustrer Ai2B étant a fortiori capables d’illustrer Ai₂B, on ne peut affirmer sans pétition de principe que c’est Ai₂B [11] qu’ils prétendent illustrer. Tout au plus peut-on noter la répugnance d’Aristote à employer des exemples qui illustreraient Ai2B sans illustrer en même temps Ai₂B, et ajouter que cette répugnance comporte un danger d’équivoque ou de malentendu.

Ces malentendus, liés aux adhérences du langage naturel, apparaissent en pleine lumière dans le domaine des preuves de non-concluance.²⁴ On sait qu’Aristote ne s’est pas contenté d’établir quelles sont les formes syllogistiques valides, mais qu’il démontre également que les couples de prémisses formellement distincts de ceux qui entrent dans les formes valides sont, de leur côté, incapables d’autoriser une conclusion. Ces procédures de rejet ont à juste titre attiré l’attention des logiciens modernes.

Le procédé qu’Aristote utilise le plus souvent, pour démontrer qu’un couple de propositions est non-concluant, a été désigné par Ross sous le nom de ‘preuve par instances contrastées’ .²⁵ Sa structure logique a été excellemment analysée par G. Patzig²⁶; il me suffira de résumer ici ce que dit cet auteur. Dire qu’un couple de prémisses appartient à l’ensemble des couples concluants, c’est dire qu’il impose nécessairement l’assignation, entre ses deux termes extrêmes, de l’une ou l’autre des quatre relations a, e, i, o, pour toute triade possible de concepts ABC. Dire qu’un couple de prémisses appartient à l’ensemble des couples non-concluants, c’est alors dire qu’il n’appartient pas à l’ensemble des couples concluants, et donc qu’il n’impose l’assignation, entre ses deux extrêmes, d’aucune de ces quatre relations. Or la nécessité d’une conclusion de type AxC est contredite par l’existence d’une triade de concepts satisfaisant à la fois le couple de prémisses considéré et une troisième proposition de forme ~AxC. On voit donc que la non-concluance d’un couple de prémisses sera démontrée s’il est possible d’exhiber quatre triades de concepts satisfaisant, d’une part, le couple en question, et d’autre part, respectivement chacune des quatre relations ~a, ~e, ~i, ~o (c’est-à-dire respectivement o, i, e, a).

Si l’on admet les lois de la subalternation, il est possible de simplifier cette preuve. En effet, la triade de concepts qui satisfait la relation AaC permet alors d’éliminer, non seulement la conclusion AoC, mais encore a fortiori la conclusion AeC; de même pour la triade satisfaisant AeC. Il suffit désormais, et c’est ainsi que procède Aristote²⁷, d’exhiber deux triades seulement pour éliminer les quatre conclusions éventuelles.

Le procédé d’Aristote a été très souvent qualifié d’extralogique, parce que [12] les triades de concepts qu’il allègue sont composées de concepts concrets, comme animal, homme, cheval.²⁸ Patzig a défendu Aristote contre cette critique, en montrant que le caractère ‘naturel’ de ces concepts n’est qu’un aspect accidentel de la preuve, et qu’Aristote aurait pu, sans rien changer à l’essence du procédé, construire artificiellement les concepts dont il avait besoin.²⁹ Prenons un exemple pour éclairer ce point. En An. Pr. I 4, 26 a 2-9, Aristote démontre la non-concluance du couple de première figure AaB.BeC en exhibant les deux triades animal, homme, cheval (qui satisfait les prémisses et AaC) et animal, homme, pierre (qui satisfait les prémisses et AeC).³⁰ En développant les suggestions de Patzig, on peut indiquer une construction possible du troisième terme de chaque triade, à partir des deux premiers: satisfera AaC le concept ‘artificiel’ animal-non-homme (dont le concept ‘naturel’ cheval, choisi par Aristote, n’est qu’un sous-concept); satisfera AeC le concept non-homme-non-animal (dont le concept ‘naturel’ pierre n’est à son tour qu’un sous-concept). En somme, une fois donnés deux concepts ‘naturels’ A et B, satisfaisant la majeure AaB, on peut toujours trouver un concept C qui satisfasse la mineure BeC et AaC, ce sera (A. ~B), et un autre concept C qui satisfasse BeC et AeC, ce sera (~A. ~B).

On peut même faire un pas de plus dans le sens indiqué par Patzig, et construire artificiellement, non pas seulement l’un des concepts à partir des deux autres, mais deux des concepts à partir du seul troisième; ainsi seulement écartera-t-on entièrement le reproche d’introduire en logique des propositions qui, comme ‘animal convient à tout homme’ , ne sont pas des thèses logiques. Dans l’exemple que nous avons pris, il y a un instant, la première triade serait A, (A.B), (A. ~B) qui satisfait formellement les conditions requises, puisque la loi non-logique ‘animal appartient à tout homme’ est remplacée par la loi logique ‘A appartient à tout (A. B)’ ; la seconde triade serait alors A, (A. B), (~A. ~B). Ce procédé de construction peut être généralisé, et l’on obtiendra dans tous les cas les triades requises par sommes ou produits logiques de variables conceptuelles. Si Aristote a préféré travailler avec des concepts ‘naturels’ , désignés par un mot unique du langage courant, on peut admettre avec Patzig que c’est pour rendre ses démonstrations intuitivement plus évidentes; mais il est permis de supposer que c’est par des procédés de construction du type décrit ci-dessus qu’il a déterminé les concepts ‘naturels’ dont il a fait usage.

La preuve par instances contrastées n’est cependant pas la seule qu’Aristote ait utilisée pour ses démonstrations de non-concluance. On sait en [13] effet qu’il emploie aussi, à l’occasion, un autre procédé, qui a retenu l’attention parce qu’il est le symétrique négatif de la démonstration de validité d’un mode concluant, par  ‘réduction’ à un autre déjà connu ou admis comme concluant: la non-concluance de certains couples de prémisses, de même, entraîne celle de certains autres. Cette amorce d’un système déductif du rejeta donné lieu à des recherches célèbres chez Lukasiewicz et son école.³¹ L’aspect du problème qui nous retiendra ici sera moins l’analyse du procédé lui-même que celle des circonstances dans lesquelles Aristote l’emploie, et des modalités de cet emploi.

Aristote appelle ce procédé la preuve par l’indéterminé.³² La possibilité de déduire, à partir d’une non-concluance déjà connue, une non-concluance nouvelle, repose en effet sur ce qu’il désigne sous le nom d’indétermination de la particulière, c’est-à-dire sur le fait qu’elle peut être vraie aussi bien si sa subalternante est fausse que si cette subalternante est vraie; en d’autres termes, AoB supposé vrai A ne convient pas à quelque B) n’implique ni n’exclut la vérité de AeB (A peut, soit ne convenir à aucun B, et donc a fortiori ne pas convenir à quelque B, soit ne pas convenir à quelque B et convenir à quelque autre B). Il en est de même pour l’affirmative.³³ On voit aisément que cette indétermination de la particulière n’appartient qu’à la particulière minimale, et qu’elle est solidaire de la légitimité de la subalternation. Elle permet de déduire, de la non-concluance déjà connue d’un couple de prémisses comportant une universelle, la non-concluance du couple que l’on obtient en remplaçant cette universelle par la particulière subalternée; en effet, l’indétermination de la particulière implique que le second couple ne saurait être concluant sans que le premier ne le soit, ce qui est [14] déjà connu comme faux. La loi propositionnelle ici en jeu, comme l’a montré Patzig (op. cit., p. 193, n. 2), est:

[~(p.q → r) · (q → s)] → ~(p.s → r).

Aristote n’a pas systématisé ce procédé, qui aurait pu théoriquement s’appliquer à tous les couples non-concluants comportant une particulière. Il ne l’emploie que lorsque son procédé habituel, la preuve par instances contrastées, rencontre certains obstacles, qui précisément sont eux aussi relatifs à la question de l’interprétation de la particulière. Les occurrences de la preuve par l’indéterminé sont au nombre de sept: (1) An. Pr. I, 4, 26 b 14-20; 2) 26 b 20-21; (3) 5, 27 b 20-23; (4) 27 b 28; (5) 28 b 28-31; (6) 29 a 3-6; 7) 15, 35 b 11. Ils concernent respectivement la non-concluance des couples a-o et e-o en première figure, e-o et a-i en deuxième figure, a-o et e-o en troisième figure, et enfin a-o en première figure avec majeure contingente et mineure assertorique. Ces passages ont souvent été étudiés; mais ils n’ont jamais, à ma connaissance, fait l’objet d’un examen qui les prenne tous systématiquement en considération.³⁴

Les cas (1) et (2) d’une part, (3), (d), (5), (6) d’autre part ne présentant pas de différences sous le rapport qui nous intéresse, il nous suffira d’ailleurs de trois analyses pour tirer le bénéfice de cet examen.

La première occurrence de la preuve par l’indéterminé apparaît dans les démonstrations de non-concluance des couples a-o et e-o en première figure (An. Pr. I, 4, 26 a 39 s.). Elle se présente ici comme une preuve secondaire, juxtaposée à une preuve par instances contrastées; celle-ci n’est cependant pas du type habituel; les conditions particulières du cas à l’étude sont responsables à la fois de l’adoption par Aristote d’une variante insolite (et d’ailleurs logiquement fautive) de la preuve par instances contrastées et de l’addition, également insolite, d’une preuve supplémentaire par l’indéterminé.

Lorsque les prémisses sont de forme AaB. BoC ou AeB. BoC, commence Aristote, il n’y a pas de syllogisme.³⁵ Dans le premier cas, ajoute-t-il, le majeur A pourra être lié au mineur C aussi bien par la relation a que par [15] la relation e³⁶; ce qui constitue l’amorce usuelle d’une preuve par instances contrastées.³⁷

Mais cette preuve ne s’effectue pas comme à l’accoutumée. Au lieu d’exhiber deux triades de concepts, satisfaisant l’une AaC, l’autre AeC, Aristote en exhibe une seule (animal, homme, blanc), dont on vérifiera aisément qu’elle satisfait bien AaB. BoC, mais qu’elle ne satisfait ni AaC, ni AeC, mais bien AiC et AoC en même temps. Il poursuit alors en construisant le concept ‘blanc-non-homme’ (C. ~B), qui est un sous-concept du mineur blanc, puis détermine à l’intérieur de ce concept ‘artificiel’ deux concepts ‘naturels’ dont l’un, cygne, est A, l’autre, neige, est ~A.³⁸ Le majeur animal étant universellement affirmé de cygne et universellement nié de neige, Aristote estime que l’absence de conclusion syllogistique est démontrée.³⁹

Cette procédure inhabituelle s’explique par la répugnance d’Aristote à utiliser, dans ses exemples concrets, des particulières autres que maximales. Dans le cas qui nous occupe, on peut trouver une triade de concepts satisfaisant à la fois la mineure BoC en un sens maximal et la relation AaC⁴⁰; mais on ne peut en trouver qui satisfasse à la fois Bo₂C et AeC, parce que Bo₂C implique BiC et que le couple AaB.BiC donne par Darii la conclusion AiC, laquelle contredit la relation cherchée AeC. La seule solution serait d’adopter une triade qui satisferait la mineure en un sens minimal seulement, c’est-à-dire sans impliquer BiC; en d’autres termes, cette mineure satisferait BeC, et donc aussi Bo₁C, mais seulement a fortiori.⁴¹

Aristote a cru éviter cette nécessité, et pouvoir mener à bien sa preuve par instances contrastées, en recourant à un artifice dont Patzig a bien montré le caractère illégitime.⁴² Pour le dire en deux mots, il a cherché à concilier les inconciliables, en jouant à la fois sur deux tableaux, celui de l’interprétation maximale de la particulière et celui des exigences de la preuve par instances contrastées. Sa triade initiale (animal, homme, blanc) satisfait Bo2C; mais elle ne permet aucune relation universelle entre les extrêmes. Les deux triades qui s’y substituent (animal, homme, cygne; animal, homme, neige) [16] satisfont bien AaC et AeC; en revanche, elles ne satisfont plus Bo₂C, mais seulement Bo₁C. Autrement dit, le mineur est blanc lorsqu’il faut satisfaire Bo2C, cygne (ou neige) lorsqu’il faut faire aboutir la preuve; la substitution étant simplement autorisée par le fait que cygne et neige sont inclus dans blanc (sont quelque blanc). Aristote a cru à tort que cette substitution pouvait se faire sans modification de la quantité de la mineure: en fait, comme le dit Patzig, la substitution transforme la mineure de particulière en universelle.⁴³ On perd donc d’une main ce qu’on gagne de l’autre; seul un quaternio terminorum permet de dissimuler la situation, et de croire qu’on a tout gagné.

Après quelques lignes qui transposent ce procédé au cas du couple AeB.BoC⁴⁴, Aristote passe à une nouvelle preuve, introduite par le mot έτι: c’est la preuve par l’indéterminé. Le raisonnement est le suivant: BoC est vrai aussi quand BeC est vrai (il s’agit donc de Bo1C); si le couple AaB.BoC était concluant, le couple AaB.BeC devrait donc l’être aussi; or on a démontré plus haut⁴⁵ qu’il ne l’était pas; donc AaB.BoC ne l’est pas non plus. Ce raisonnement est également appliqué, dans les lignes suivantes, au couple AeB.BoC.

La structure logique de la preuve par l’indéterminé ayant été parfaitement analysée par Patzig⁴⁶, je me contenterai de noter la situation paradoxale où se trouve ici Aristote.⁴⁷ Par attachement aux connotations maximales de la particulière, il a remanié, de façon d’ailleurs erronée, sa preuve par instances contrastées; puis il a présenté comme une preuve alternative une démonstration fondée sur l’indétermination de la particulière, c’est-à-dire sur l’abandon de ses connotations maximales. Cette attitude sans cohérence était vouée à se transformer; nous allons voir maintenant qu’elle l’a fait.

Dans le cas (3) de la liste que nous avons donnée ci-dessus (5, 27 b 12 sq.), Aristote se propose de démontrer la non-concluance du couple de deuxième figure MeN. Mo X. Il commence par dire que ce couple est compatible avec les deux relations NaX et NeX entre les extrêmes, ce qui annonce une démonstration par instances contrastées.⁴⁸ Il donne ensuite une première triade (noir, neige, animal)⁴⁹, qui satisfait les prémisses (MoX au sens maximal) et la relation NeX entre les extrêmes.⁵⁰ Mais il ajoute, et cela est très digne de remarque, qu’on ne peut trouver de triade satisfaisant NaX si la particulière MoX a le sens maximal.⁵¹ Il en donne aussitôt la démonstration: la relation cherchée NaX, couplée avec la première prémisse MeN, livre par Celarent (avec renversement de l’ordre des prémisses) la conclusion MeX; or celle-ci contredit MiX, et donc Mo₂X.⁵²

Ce développement marre une conscience beaucoup plus nette des données du problème. Rien n’empêchait en effet Aristote de procéder comme il l’avait fait dans le premier cas que nous ayons examiné⁵³; il n’en a rien fait. Il est curieux de constater, cependant, qu’après avoir signalé clairement la condition sous laquelle échoue nécessairement la preuve par instances contrastées, il n’a pas songé à faire aboutir cette preuve en levant cette condition, comme il aurait pu également le faire.⁵⁴ Au lieu de cela, il prend son parti de l’échec de la preuve par instances contrastées, et se rabat sur la preuve par l’indéterminé, présentée comme un recours rendu nécessaire par cet échec: “Dans ces conditions, donc, il n’est pas possible de prendre des termes ‘adéquats’, mais il faut faire une démonstration par l’indéterminé”.⁵⁵ Cette démonstration ne fait pas de difficulté: la non-concluance de MeN. MeX ayant été démontrée par instances contrastées en 27 a 20-23, celle de MeN. MoX s’en déduit.

Malgré le progrès accompli, la situation dans laquelle se trouve maintenant [18] Aristote n’est pas moins incohérente que dans le cas précédent. En effet, il présente la preuve par l’indéterminé comme un recours contre l’échec de la preuve par instances contrastées.⁵⁶ Or c’est l’interprétation maximale de la particulière qui rendait cet échec nécessaire, et Aristote l’a bien vu; mais il est évident que cette interprétation rendrait également impossible la preuve par l’indéterminé, puisque l’universelle n’implique pas la particulière maximale. Autrement dit, la preuve par l’indéterminé n’aboutit que si on lève la condition qui avait fait échouer la preuve par instances contrastées, et la preuve par instances contrastées aurait réussi si l’on avait admis les conditions sous lesquelles peut aboutir la preuve par l’indéterminé. Les deux preuves sont, en fait, condamnées à réussir ou à échouer ensemble; et c’est une erreur de voir en l’une un remède à l’échec de l’autre.

Avant de passer à l’étude du cas (7), qui nous montrera que l’attitude d’Aristote s’est encore modifiée une fois, il peut être de quelque profit d’examiner quelques-uns des commentaires qui ont été consacrés à notre problème; le moment est bien choisi pour le faire, puisque, comme je l’ai dit, ces commentaires laissent régulièrement ce cas (7) de côté.

H. Maier, commentant le texte que nous venons d’analyser, écrit: “Cette observation [l’indétermination de la particulière] aurait donné la possibilité de mener à son terme la démonstration initiale [par instances contrastées] [...]. Cette manière de conclure sa démonstration s’est bien sûr présentée originairement à l’esprit d’Aristote. Mais au lieu de poursuivre ainsi, il interrompt sa démonstration initiale. La représentation du caractère indéterminé de la particulière négative lui rappelle que cette propriété permet d’effectuer une démonstration indépendante. Aussi reprend-il sur nouveaux frais: ἐκ δὲ τοῦ ἀδιορίστου δεικτέον.”⁵⁷ Cette reconstruction psychologique des processus mentaux d’Aristote n’est pas très convaincante: Aristote aurait-il interrompu sa démonstration initiale s’il avait vu la possibilité de la mener jusqu’à son terme? Aurait-il présenté la seconde preuve comme un remède à l’échec de la première s’il avait vu qu’elle contenait le moyen d’éviter cet échec? Cela n’est guère vraisemblable.

Lukasiewicz commente notre texte avec rapidité, et son commentaire n’est pas différent de celui de Maier; après avoir noté que la preuve par instances contrastées pouvait aisément être menée à son terme, il ajoute: [19] “Aristote, cependant, ne finit pas sa preuve de cette manière, parce qu’il voit une autre possibilité.”⁵⁸ Un mode de rédaction aussi versatile, interrompu et infléchi par des idées de traverse, est d’autant moins vraisemblable de la part d’Aristote que le cas (1), laissé de côté par Lukasiewicz, permet d’en écarter l’hypothèse: dans ce cas (1), en effet, la vision d’une “autre possibilité” n’avait pas empêché Aristote de mener jusqu’à son terme, au prix d’un effort laborieux et d’ailleurs malheureux, la preuve déjà amorcée par instances contrastées.

T. Sugihara, de son côté, traite simultanément des six occurrences de la preuve par l’indéterminé, effaçant ainsi toute différence entre les deux situations que nous avons jusqu’à présent distinguées. Il écrit: “Concernant ces six modes, il est impossible de prouver par instances contrastées qu’il n’y a pas syllogisme si la prémisse est particulière, tandis que c’est possible si la prémisse est indéfinie [...]. Tous ces énoncés d’Aristote sur les modes ne peuvent être interprétés correctement que si sa ‘particulière’ est bilatérale [maximale] et son ‘indéfinie’ unilatérale [minimale].”⁵⁹ Aristote ne dit nullement que la non-concluance de ces six modes est indémontrable par instances contrastées si la prémisse est particulière: dans le premier cas, il effectue cette démonstration (en se trompant, mais peu importe); dans le second cas, il dit qu’elle est impossible si la particulière est maximale (ou bilatérale). Il ne dit pas davantage que la non-concluance est démontrable lorsque la prémisse est indéfinie; il montre qu’elle l’est si la particulière est minimale (ou unilatérale). Ces équivoques montrent à quel point il est nécessaire de bien distinguer les deux sens aristotéliciens d’ἀδιόριστος, dont l’un désigne une propriété qui peut ou non appartenir à la particulière, tandis que l’autre désigne une proposition autre que la particulière.

G. Patzig, enfin, après avoir analysé avec une clarté inégalée le cas (1), se contente un peu rapidement de lui assimiler les cas suivants. Il écrit notamment: “Aristote utilise la preuve ἐκ τοῦ ἀδιορίστου là, et là seulement, où [...] se rencontre cette difficulté, que pour l’une des deux triades de concepts on ne peut trouver de termes qui ne satisfassent pas aussi la forme universelle de la mineure. Que ce soit bien en fait cette difficulté qui, dans de tels cas, le fasse recourir à la loi qui a été décrite [loi de dérivation d’une non-concluance à une autre], cela ressort du texte de tous ces passages. Il suffit de citer ici la preuve de non-concluance de e-o en deuxième figure [suit la traduction des lignes 27 b 16-21].”⁶⁰ Ce commentaire marque exactement [20] ce qu’il y a de commun dans les divers cas examinés, il ne rend pas justice à leurs différences.

Le cas (7) qui nous reste maintenant à examiner, figure dans la syllogistique modale (15, 35 b 11); il y est, sauf erreur de ma part, seul de son espèce. La circonstance est déjà remarquable. La liste des six occurrences de la preuve par l’indéterminé dans la syllogistique assertorique pouvait se justifier facilement, sur le plan théorique: il y en a autant que de modes concluants à mineure particulière, soit six (Darii et Ferio en première figure, Festino et Baroco en deuxième, Datisi et Ferison en troisième). En effet, si l’on remplace les mineures de ces modes par leurs subcontraires, on obtiendra des couples de prémisses qui rencontreront nécessairement l’obstacle que nous connaissons, lorsqu’on tentera de démontrer leur non-concluance par instances contrastées: la seconde prémisse, si elle est prise au sens maximal, pourra être remplacée de nouveau par sa subcontraire, et le couple deviendra bel et bien concluant. La liste des six cas est donc déterminée par substitution de i à o et de o à i dans la liste ci-dessus: a-o et e-o en première figure, e-o et a-i en deuxième, a-o et e-o en troisième. Quant aux modes dans lesquels c’est la majeure qui est particulière, ils sont concluants quelle que soit la qualité de cette majeure (Disamis et Bocardo); ils tombent donc en dehors de cette énumération.

L’isolement du cas (7), par contraste avec l’organisation en système des six premiers cas, soulève un problème sur lequel il faudra revenir. Le texte lui-même est très bref. Aristote s’y propose en l’espèce de rejeter la combinaison AaB. BoC avec majeure contingente et mineure assertorique (que nous noterons MAaB. BoC).⁶¹ Il se contente de déclarer que dans ce cas, “il n’y aura pas syllogisme. Termes d’attribution: blanc, animal, neige; de non-attribution, blanc, animal, poix. C’est en effet au moyen de l’indéterminé qu’il faut prendre la démonstration⁶².”

Ce texte appelle de nombreux commentaires. Remarquons d’abord clue rien n’empêchait théoriquement Aristote de procéder comme il l’avait fait dans le cas que nous avons étudié en dernier lieu. Annonçant une démonstration par instances contrastées⁶³, il aurait montré qu’on peut [21] trouver une triade de concepts satisfaisant les prémisses et la relation NAaC⁶⁴, mais qu’on ne peut en trouver qui satisfasse la relation NAeC si la prémisse particulière est prise dans le sens maximal; ce qu’il aurait aussitôt démontré.⁶⁵ Après quoi, il aurait eu recours à la preuve par l’indéterminé, et aurait dérivé la non-concluance de MAaB. BoC de celle de MAaB. BeC, déjà démontrée par instances contrastées en 35 a 20-24.

Au lieu de quoi, Aristote se contente de faire aboutir la preuve par instances contrastées, en exhibant deux triades de concepts, dont l’une satisfait NAaC (blanc, animal, neige)⁶⁶, et l’autre NAeC (blanc, animal, poix)⁶⁷, et dans lesquelles la mineure particulière n’est vraie qu’a fortiori (puisque animal ne convient en fait à nulle neige, et à nulle poix)⁶⁸; ce sont donc les mêmes triades que celles qui permettaient de rejeter MAaB. BeC (cf. 35 a 20-24). Et il ajoute: c’est en effet au moyen de l’indéterminé qu’il faut prendre la démonstration. Cette expression, significativement différente de celles qui ont été relevées plus haut⁶⁹, montre que l’indétermination de la particulière ne sert plus ici à fonder une ‘preuve par l’indéterminé’ qui serait le substitut d’une ‘preuve par instances contrastées’ défaillante, mais qu’elle assure désormais simplement le succès de la preuve par instances contrastées. Il n’y a plus maintenant deux preuves distinctes, mais une seule, la preuve par instances contrastées, qui utilise à l’occasion le ressort sur lequel reposait la seconde. Cette clarification de la situation correspond à une liquidation maintenant intégrale des connotations maximales de la particulière; le γάρ de la ligne 35 b 11 permet à lui seul d’affirmer que la particulière n’a désormais plus d’autre sens que celui que lui donne son statut de simple négation de l’universelle. La particulière ‘logique’ a eu quelque peine à tuer la particulière ‘naturelle’ ; mais elle a fini par y arriver.

Il manque cependant une pièce encore à notre démonstration. On a remarqué plus haut que la référence de 35 b 11 à l’indétermination de la particulière était isolée dans la syllogistique modale. Cet isolement est surprenant: il est a priori invraisemblable que la situation qui provoque cette référence ne se produise qu’une fois sur cent-vingt-huit (nombre des combinaisons possibles de prémisses modalisées). On est donc logiquement conduit à supposer qu’Aristote a dû parfois faire usage de l’indétermination de la particulière sans le dire expressément; cette manière de faire, si elle se vérifiait, permettrait de dire cette fois que la particulière maximale est non seulement morte, mais bel et bien enterrée.

La vérification de cette hypothèse exigerait une étude systématique des preuves de non-concluance en syllogistique modale, étude qui comporterait des développements et des complications considérables. Je me bornerai ici à quelques indications.

(1) La preuve par instances contrastées n’est pas la seule preuve de non-concluance utilisée par Aristote en logique modale. Lorsqu’il étudie un couple de prémisses modalisées correspondant à un couple assertorique concluant, il lui est possible de montrer que les démonstrations de concluance du couple assertorique sont rendues inefficaces par la modalisation des prémisses.⁷⁰ Or ne pas pouvoir démontrer la concluance, c’est démontrer la non-concluance.

(2) La preuve par instances contrastées garde une place importante, niais revêt des formes nouvelles, et parfois surprenantes. Dans les combinaisons de prémisses plus fortes que les combinaisons assertoriques (une ou deux prémisses apodictiques), prenons à nouveau le cas des couples qui correspondent à un couple assertorique concluant. Le seul problème est dans ces cas de savoir si le couple modalisé est capable d’une conclusion apodictique, plus forte que celle du couple assertorique, ou s’il n’est capable que de la conclusion assertorique. Dans cette situation, il n’est plus nécessaire d’exhiber deux triades de concepts, l’une pour écarter les éventuelles conclusions affirmatives, l’autre pour écarter les éventuelles conclusions négatives; si le couple assertorique a une conclusion négative, le couple modalisé ne saurait avoir une conclusion affirmative, et inversement; une triade de concepts suffira donc pour exclure la seule conclusion qui fasse sérieusement acte de candidature.⁷¹

[23]

(3) La ‘conversion complémentaire’ des contingentes⁷² introduit naturellement de grandes nouveautés dans le système. Tout d’abord, un certain nombre de couples qui n’étaient pas concluants en logique assertorique le deviennent en logique modale, grâce à la conversion complémentaire d’une prémisse négative en prémisse affirmative. En outre, cette conversion complémentaire va permettre dans certains cas à la preuve par instances contrastées de faire l’économie d’une triade de concepts, une triade unique permettant maintenant d’écarter les deux conclusions éventuelles. Supposons par exemple que l’on étudie un couple de deux prémisses contingentes. La conclusion, si conclusion il y a, ne peut être que contingente; les quatre conclusions possibles sont Ma, Me, Mi, Mo. En logique assertorique, on l’a vu, il était possible de réduire de quatre à deux le nombre des conclusions à écarter, en vertu de la subalternation (l’exclusion de o entraînant a fortiori celle de e, et l’exclusion de i entraînant a fortiori celle de a). A présent, il est toujours possible de réduire de quatre à deux le nombre des conclusions à écarter, mais c’est cette fois en vertu de la conversion complémentaire⁷³: l’exclusion de Mo est en même temps celle de Ma, l’exclusion de Mi est en même temps celle de Me. Reprenons l’exemple de la démonstration de non- concluance de MAeB. MAaC (17, 37 a 32 s.), déjà évoqué plus haut à un autre point de vue.⁷⁴ Après les deux démonstrations dont nous avons parlé, Aristote en présente une troisième par termes concrets.⁷⁵ En principe, il faudrait exhiber deux triades de concepts, dont l’une permettrait d’exclure les conclusions éventuelles MBaC et MBo₁C en satisfaisant leur négation commune NBaC ∨ NBo₁C, et dont l’autre permettrait d’exclure les conclusions éventuelles MBeC et MBi₁C en satisfaisant leur négation commune NBeC ∨ NBi₁C. Mais le caractère disjonctif de ces négations va permettre à Aristote d’utiliser la même triade de concepts pour exclure les deux couples de conclusions éventuelles. En effet, une triade dont les extrêmes satisferaient [24] la relation NBeC (dans l’exemple d’Aristote, A blanc, B homme, C cheval) satisfera le second terme de la première disjonction (par subalternation NBeC → NBo₁C), et donc cette disjonction elle-même; elle satisfera également le premier terme de la seconde disjonction, et donc cette disjonction elle aussi. Les quatre solutions contingentes possibles sont éliminées d’un seul coup par la production d’une triade dont les extrêmes sont liés par une relation apodictique.

(4) En analysant le seul passage de la logique modale où Aristote fasse explicitement recours à l’indétermination de la particulière (35 b 11), nous avons vu qu’Aristote y prouvait qu’il avait fini par comprendre que les mêmes triades de concepts pouvaient lui servir pour démontrer la non-concluance d’un couple de prémisses comportant une universelle et pour démontrer (“grâce à l’indéterminé”) celle du couple obtenu par substitution à cette universelle de sa subalterne: les triades blanc-animal-neige et blanc-animal-poix avaient servi contre MAaB. BeC en 35 a 20-24, elles resservent contre MAaB. BoC en 35 b 8-11. Cette découverte libère Aristote du souci de trouver des triades de concepts distinctes pour chacune des démonstrations de non-concluance qu’il veut effectuer. Une fois découverte une triade appropriée à la démonstration de non-concluance d’une ‘combinaison-mère’ , cette triade sera considérée comme démonstrative de la non-concluance de toutes les ‘combinaisons-filles’ ; j’entends par combinaisons-filles celles qu’on obtient en remplaçant les prémisses de la combinaison-mère par celles qu’elles impliquent par subalternation, ou qui leur sont équivalentes par conversion complémentaire. Le jeu particulier et le jeu combiné de ces deux facteurs, subalternation et conversion complémentaire, fera nécessairement que le nombre des combinaisons-filles sera considérable; ainsi s’expliquent ces véritables ‘fournées’ de démonstrations de nonconcluance qu’Aristote effectue d’un seul coup, en disant que les mêmes termes concrets sont déterminants dans tous les cas rassemblés.⁷⁶

(5) Si deux termes concrets liés en fait par une relation universelle a ou e peuvent être considérés (et Aristote le croit maintenant sans arrière-pensée) comme satisfaisant a fortiori la relation particulière i₁ ou o₁, cette situation comporte une contrepartie: il faut admettre aussi que deux termes concrets liés en fait par une relation particulière maximale (i₁. o₁) soient considérés [25] comme pouvant satisfaire les relations universelles a ou e. Par exemple, s’il est vrai qu’en fait quelque animal est blanc et quelque animal n’est pas blanc, les propositions “Tout animal est blanc” et “Nul animal n’est blanc” sont toutes deux fausses, mais non impossibles. Dès lors, le premier pas franchi par Aristote pouvait se prolonger d’un second: le premier avait consisté à admettre qu’une relation particulière est satisfaite par deux termes concrets qui la satisfont a fortiori; le second consistera à admettre qu’une relation universelle est satisfaite par deux termes concrets qui pourraient (bien qu’ils ne le fassent pas en fait) la satisfaire. Cette procédure subtile est utilisée dans le rejet de NAaB. AeC → NBeC (10, 30 b 18 sq.), que nous avons évoqué plus haut.⁷⁷ La triade qui permet de rejeter la conclusion NBeC est en effet animal, homme, blanc. Cette triade est donnée comme satisfaisant AeC, c’est-à-dire la mineure assertorique ‘animal n’appartient à aucun blanc’ ; et en effet, explique Aristote, “il peut se faire qu’animal n’appartienne à aucun blanc”.⁷⁸ Passant hardiment de l’assertion d’une possibilité à la possibilité d’une assertion, Aristote use de ce stratagème pour montrer que la conclusion BeC (homme n’appartient à aucun blanc), qui de son côté est elle aussi fausse, mais non impossible, suit nécessairement des prémisses supposées vraies, mais n’est pas en elle-même apodictique. Dans ce nouvel avatar, la preuve par termes concrets prend un sens radicalement nouveau: le lecteur d’Aristote n’est plus invité à constater, dans le monde réel, les relations logiques qu’entretiennent mutuellement les animaux, les hommes, les couleurs, mais à se transporter dans un monde imaginaire, mais possible, où par exemple aucun être blanc ne serait vivant, et à se demander ce qui en résulterait.⁷⁹ Il est inutile de souligner combien la preuve par termes concrets, dans cet élargissement, perd de son ‘évidence’ intuitive; inutile également de faire remarquer combien il est facile à Aristote, retrouvant le monde réel où quelques êtres blancs seulement sont inanimés, de déclarer que la non-concluance du couple subalterné NAaB. AoC se démontre “à l’aide des mêmes termes qui ont servi pour les syllogismes universels”.⁸⁰ Le contraire aurait été étonnant.

Au cours de l’évolution qui vient d’être retracée, Aristote a donc progressivement et parallèlement liquidé les connotations maximales de la particulière, aboli la distinction entre une ‘preuve par instances contrastées’ et une ‘preuve par l’indéterminé’ , assoupli les critères en vertu desquels on [26] peut reconnaître que deux termes concrets ‘satisfont’ une relation donnée. Il est heureux qu’il n’ait pas eu la volonté ou le loisir de récrire l’ensemble des Premiers Analytiques pour le mettre en harmonie avec le dernier état de sa pensée logique: l’édifice qu’il nous a laissé a gardé son échafaudage. Parlant de ses prédécesseurs, il a souvent dit qu’ils avaient été parfois contraints “par la chose même” à modifier leurs positions primitives⁸¹; il a eu lui-même, comme on voit, le bon goût de ne pas se dérober à cette contrainte⁸².

Notes

1. Cf. J. Lukasiewicz, Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic, 2nd ed. enlarged, Oxford, Clarendon Press, 1957, p. 15: “The Aristotelian logic is formal without being formalistic, whereas the logic of the Stoics is both formal and formalistic”. ↵

2. Cf. Ammonius, In Aristotelis Analyticorum Priorum Librum I Commentarium, ed. Wallies, Berlin, 1899, p. 10, l. 36 s., cité par Lukasiewicz, op. cit., p. 13, n. 1. ↵

3. R. Blanché, Introduction à la logique contemporaine, Paris, Colin, 1957, p. 18. ↵

4. Lukasiewicz, op. cit., p. 14.Il serait plus exact de dire: ‘appartient à tout’ , ‘n’appartient à aucun’ , etc. Je noterai ci-dessous ces relations à l’aide des voyelles traditionnelles a, e, i, et o. ↵

5. Lukasiewicz, op. cit., p. 16. ↵

6. Cf. An. Pr. I, 39, 49 b 3: δεῖ δὲ καὶ μεταλαμβάνειν ἃ τὸ αὐτὸ δύναται, ὀνόματα αντ’ ὀνομάτων καὶ λόγους ἀντὶ λόγων καὶ ὄνομα καὶ λόγον.Lukasiewicz a tort de citer cette phrase en l’interrompant après λόγων (op. cit., p. 18, n. 2), donnant aussi faussement l’impression qu’Aristote n’autorise que les échanges “words for words and phrases for phrases”, alors qu’il admet aussi bien les échanges ‘mots pour expressions’ et vice versa. Notons aussi qu’en commentant un exemple, quelques lignes plus bas, Aristote précise explicitement que le signifié des termes substituables est identique (ταὐτὸν γὰρ τὸ σημαινόμενον, 49 b 8). ↵

7. R. Blanché, op. cit., p. 18. ↵

8. “These troublesome propositions”, disait J. Venn, Symbolic Logic, Londres 1881, p. 169, cité par R. Blanché, Structures intellectuelles, Paris, Vrin, 1966, p. 38. ↵

9. Cf. l’exposé récent de W. et M. Kneale, The Development of Logic, Oxford, 1962, p. 56-61. ↵

10. Cf. sur ce point R. Blanché, Structures intellectuelles, notamment le chapitre III, p. 35-46. ↵

11. J’adopte ici la notation utilisée dans un ouvrage auquel cette étude se réfère constamment: Günther Patzig, Die aristotelische Syllogistik, 2e éd., Göttingen, Vandenhoeck und Ruprecht, 1963. La minuscule désigne l’une des quatre relations traditionnelles a, e, i, o; les majuscules désignent les variables de termes, celle qui figure à gauche de la minuscule représentant le prédicat, et celle qui figure à droite représentant le sujet. AaB doit donc être lu ‘A appartient à tout B’ , ou encore ‘Tout B est A’ . Sur les justifications de cette notation, qui reproduit l’usage aristotélicien le plus fréquent, cf. Patzig, op. cit., p. 19 s. ↵

12. Cf. Blanché, Structures intellectuelles, p. 36-37. ↵

13. Lukasiewicz, op. cit., p. 10. ↵

14. Une solution, naturellement meilleure sur le plan théorique, consiste à modifier la structure quadratique traditionnelle pour faire place à deux types distincts de particulières, satisfaisant à eux deux les trois relations (a), (b) et (c). Tel est l’hexagone logique de M. Blanché, où figurent, outre les quatre postes traditionnels a, e, i, o, deux postes nouveaux: y, défini comme la conjonction de i et de o, et u, défini comme la contradictoire de y, c’est-à-dire comme la disjonction de a et de e. Cf. sur ce point, outre les Structures intellectuelles déjà citées, les deux exposés préliminaires de R. Blanché: ‘Sur l’opposition des concepts’, in Theoria 19 (1953) 89-130, et ‘Opposition et négation’, in Revue philosophique 147 (1957) 187-216; voir également G. Kalinowski, ‘Axiomatisation et formalisation de la théorie hexagonale de l’opposition de M. R. Blanché’, in Les Études philosophiques 22 (1967) 203-209. Si je préfère ici poser en termes de choix entre plusieurs ‘carrés’ possibles un problème dont M. Blanché a su intégrer les éléments dans une structure plus complexe et plus compréhensive, c’est, comme on le verra plus clairement par la suite, parce que cette présentation a paru susceptible d’éclairer la nature des problèmes qui se sont posés à Aristote. Signalons qu’un système d’oppositions où figurent les mêmes postes que ceux de M. Blanché, mais désignés sous d’autres noms et schématisés d’une façon différent; a été présenté par Paul Jacoby, ‘A triangle of opposites for types of propositions in Aristotelian Logic’, in The New Scholasticism 24 (1950), 32-56, avec l’ambition (d’une cohérence peut-être discutable) d’être “fidèle à la théorie logique d’Aristote lui-même, en comblant quelques petites lacunes pour satisfaire aux exigences d’un schéma complet et cohérent” (p. 47). ↵

15. Les deux particulières signifient: ‘A appartient à quelque B et n’appartient pas à quelque (autre) B’ ; les deux universelles signifient: ‘A appartient à tout B ou n’appartient à nul B’ , ou en d’autres termes: ‘A appartient universellement à B, soit affirmativement soit négativement’ . On peut donc dire qu’il n’y a plus ici de carré d’opposition, mais un simple segment d’opposition, dont les termes sont a₁ ∨ e₁ d’une part, i₁ ⋅ o₁ d’autre part. La combinaison de ce segment avec le carré traditionnel donnerait précisément l’hexagone de M. Blanché. ↵

16. On pourrait montrer qu’Aristote s’est trouvé dans le domaine de la modalité, devant un problème de choix structuralement analogue. La proposition modale ‘il est possible que p’ est en effet engagée, dans son usage naturel, en deux relations incompatibles; d’une part, elle est impliquée par sa ‘subalternante modale’ , ‘il est nécessaire que p’ , puisque, si un état de choses est dit nécessaire, on doit apparemment affirmer qu’il est a fortiori possible; d’autre part, elle équivaut à sa ‘subcontraire modale’, ‘il est possible que non-p’, puisque, si non-p n’était pas possible, on affirmerait de p qu’il est nécessaire, et non possible. Mais on ne peut admettre les deux relations à la fois, puisque la nécessité de p impliquerait médiatement la possibilité de non-p. Il faut donc choisir entre une interprétation minimale de la problématique (‘il est au moins possible que p’) et une interprétation maximale ( ‘il est au moins et au plus possible que p’). Comme on sait, les hésitations d’Aristote ont pris dans le domaine de la modalité une forme plus nette et plus spectaculaire que dans le domaine de la qualité; il n’y a pas sacrifié l’interpré¬tation maximale. ↵

17. Je conteste donc directement les conclusions de Takeo Sugihara, Particular and indefinite proposition in aristotelian logic, in Memoirs of Liberal Arts College, Fukui University 3 (1954) 77-86. Cet article est venu à ma connaissance par une référence de I.M. Bochenski, A History of Formal Logic, Notre-Dame Press, 1961 (traduction par Ivo Thomas de Formale Logik, Freiburg-München, Alber 1956), p. 58 et 472; j’ai pu en consulter un tiré à part grice à l’obligeance de M. Sugihara lui-même, et à l’aimable entremise de M. Takefumi Tokoro, que je remercie vivement tous deux. L’article est en japonais; il comporte un résumé anglais de deux pages, d’après lequel j’ai travaillé, et que je citerai ici littéralement, parce que Bochenski fait dire à l’auteur exactement le contraire de ce qu’il dit. Cf. Bochenski, op. cit., p. 58; “In the particu1ar sentence, ‘some’ means ‘at least one, not excluding all’ . Whereas, as Sugihara has recently shown, an indefinite sentence should probably be interpreted in the sense: ‘at least one A is B and at least one A is not B’ ”. La thèse de M. Sugihara est au contraire: “Aristotelian ‘particular’ is bilateral [i. e. ‘A applies to some of B and does not apply to the others of B’], and ‘indefinite is unilateral’ [i.e. ‘A applies to some of B ’]”. J’espère que l’exactitude du résumé anglais n’est pas à mettre en cause. Je signalerai et discuterai ci-dessous les trois arguments que donne M. Sugihara à l’appui de sa thèse. ↵

18. Λέγω δὲ καθόλου μὲν τό παντὶ ἤ μηδενὶ ὑπάρχειν, ἐν μέρει δὲ τὸ τινὶ ἢ μὴ τινὶ ἤ μὴ παντὶ ὑπάρχειν, ἀδιόριστον δὲ τὸ ὑπάρχειν ἤ μὴ ὑπάρχειν ἄνευ τοῦ καθόλου ἤ κατὰ μέρος. Je traduis ici ἀδιόριστον par indéfini, conformément d’ailleurs à l’usage. Au point de vue logique, on sait qu’Aristote assimile l’indéfiuie à la particulière: cf. par exemple I, 4. 26 a 28-30, 32-33, 39, etc. ↵

19. Cf. par exemple I, 4, 26 a 37, 26 b 4-5. ↵

20. Cf. An Pr. II, 15, 63 b 23-30. Sur la subalternation, cf. Top. II, 1, 109 a 3-6; III, 6, 119 a 34 s, ; et les textes que nous retrouverons ci-dessous, An Pr. I, 4, 26 b 15-16 et 5, 27 b 21-22. ↵

21. Cf. An Pr. II, 15, 63 b 27-28: τὸ γὰρ τινὶ τῷ οὐ τινὶ κατὰ τὴν λέξιν ἀντίκειται μόνον. ↵

22. Cf. la liste des 14 exemples de particulières concrères figurant dans la syllogistique assertorique, in Sugihara, art. cit. (il faudrait cependant transférer l’exemple neige-blanc du second groupe au premier). ↵

23. Cf. à ce sujet les remarques importantes de G. Patzig, op. cit., p. 191: “Umgangssprachlich bedeutet freilich ein Satz der Form ‘A kommt einigen B nicht zu’ fast stets, dass einige B allerdings A sind. (Dies ist indessen noch eine oberflächliche Ansicht der Sache: Bedeuten kann der Satz AoB auch umgangssprachlich nicht, dass auch AiC [sic; lire AiB] gilt. Aber er wird meist nur in Situationen benutzt, in denen auch AiC [même remarque] gilt, und die Umgangssprache hat die Tendenz, die gewöhnliche Situation, in der ein Satz verwendet wird, seiner Bedeutung zuzurechnen ” (Souligné par l’auteur). ↵

24. Cf. sur cette partie de la syllogistique Lukasiewicz, op. cit., p. 67-72, p. 94-99, p. 100-132; Patzig, op. cit., p. 180-197. ↵

25. Cf. Aristotle’s Prior and Posterior Analytics, a revised text with introduction and commentary by W. D. Ross, Oxford, Clarendon Press, 1949, p. 302. ↵

26. G. Patzig, op. cit., p. 187-190. ↵

27. Cf. par exemple An. Pr. I, 4, 26 a 2-9, où la relevance des lois de la subaltemation est expressément soulignée (καὶ γὰρ παντὶ καὶ μηδενὶ ἐνδέχται τὸ πρῶτον τῷ ἐσχάτῳ ὑπάρχειν, ὥστε οὔτε τὸ κατὰ μέρος οὔτε τὸ καθόλου γίνεται ἀναγκαῖον). ↵

28. Cf. Lukasiewicz, op. cit., p. 72: “This procedure is correct, but it introduces into logic terms and propositions not germane to it. ‘Man’ and ‘animal’ are not logical terms, and the proposition ‘All men are animals’ is not a logical thesis. Logic cannot depend on concrete terms and statements”. Critique de même type chez Ross, op. cit., p. 28-29, et chez beaucoup d’autres. ↵

29. Cf. Patzig, op. cit., p. 196. ↵

30. Rappelons qu’en première figure, les termes des triades sont donnés dans l’ordre: majeur A, moyen B, mineur C. ↵

31. Cf. Lukasiewicz. op. cit., p. 94-99, et l’ensemble du chapitre V. ↵

32. Ἐκ τοῦ ἀδιορίστου. Je traduis ici par indéterminé, pour bien marquer la différence entre cet emploi du mot et celui que j’ai traduit ci-dessus par indéfini (cf. note 18). La nécessité de cette différenciation sera justifiée dans la note suivante. ↵

33. Cf. An. Pr. I, 4, 26 b 14-16: ἐπεὶ ἀδιόριστον τὸ τινὶ τῷ Γ τὸ Β μὴ ὑπάρχειν, ἀληθεύεται δέ, καὶ εἰ μηδενὶ ὑπάρχει καὶ εἰ μὴ παντί, ὅτι τινὶ οὐχ ὑπάρχει. 5, 27 b 21-22; ἐπεὶ γὰρ ἀληθεύεται τὸ τινὶ μὴ ὑπάρχειν τὸ Μ τῷ Ξ καὶ εἰ μηδενὶ ὑπάρχει. 6, 28 b 28: ἀδιορίστου γὰρ ὄντος τοῦ τινὶ μὴ ὑπάρχειν καὶ τὸ μηδενὶ ὑπάρχον ἀληθὲς εἰπεῖν τινὶ μὴ ὑπάρχειν. Cette indétermination n’est naturellement pas propre à la particulière négative: sur le cas de l’affirmative, cf. 5, 27 b 23-28. Il est tout à fait impossible d s’appuyer sur ces textes pour identifier la particulière minimale avec 1’ ‘indéfinie’ aristotélicienne, comme le fait T. Sugihara: le mot ἀδιόριστος ne peut avoir la même signification quand il dénomme une proposition non quantifiée (la proposition indéfinie, cf. ci-dessus note 18) et quand il dénote une propriété appartenant à la proposition quantifiée particulièrement (l’indétermination de la proposition particulière, interprétée au sens minimal). La distinction de ces acceptions a été parfois bien aperçue (Cf. Waitz, Organon, Leipzig, 1844, t. 1. p. 383; H. Maier, Die Syllogistik des Aristoteles, Tübingen, 1896, t. 1, p. 162-163); mais elle a souvent aussi été masquée, parce que l’on a confondu ce que dit ici Aristote de l’indétermination de la particulière avec ce qu’il dit ailleurs (cf. ci-dessus, note 18) de l’équivalence logique entre indéfinie et particulière. Cette équivoque du mot ἀδιόριστος a même contribué à défigurer entièrement le texte d’un passage des Topiques (III, 6, 120 a 6 s.) dans la presque totalité de la tradition manuscrite, dans la totalité des éditions modernes et chez tous les commentateurs qui s’en sont occupés; une correction malencontreuse, et qui remonte très haut dans le temps, a transformé en indéfinie ce qui dans ce texte n’était que particulière indéterminée; Pour le détail de cette question, je ne puis ici que me permettre de renvoyer à mon édition des Topiques, t. 1, Paris, Les Belles Lettres, 1967, p. 77 et 163-164. ↵

34. Par exemple, Lukasiewicz ne traite que du cas (3); Patzig analyse très précisément le cas (1), mais signale plus rapidement le cas (3) et ignore le cas (7); Sugihara n’énumère que les cas (1) à (6). Le cas (7) doit à sa place dans les chapitres de synogistique modale la négligence dont il a été l’objet; mais les commentateurs de la syllogistique modale eux-mêmes n’y ont pas prêté grande attention. Albrecht Becker (Die aristotelische Theorie au Möglichkeitsschlüsse, Berlin, 1933) le déclare exactement semblable aux cas présentés dans la synogistique assertorique (“In genau dem selben Sinn... aufzufassen”, p. 71, n. 2). Nous verrons qu’il n’en est rien. Le commentaire de Ross ad locum (op. cit., p. 343-344) est lui aussi insensible aux particularités de ce passage. ↵

35. Οὐδ’ ὅταν τὸ μὲν πρὸς τῷ μείζονι ἄκρῳ καθόλου γένηται ἤ κατηγορικὸν ἤ στερητικόν, τὸ δὲ πρὸς τῷ ελάττονι στερητικὸν κατὰ μέρος, οὐκ ἔσται συλλογισμὸς ἀδιορίστου τε καὶ ἐν μέρει ληφθὲντος. Les six derniers mots sont supprimés par Ross, comme “a pointless repetition of the previous line ” (op. cit., p. 304), ce qui n’est pas un bon argument: la ligne précédente dit que la mineure est particulière négative, celle-ci que le cas serait le même si elle était indéfinie. Cette correction discutable est tacitement approuvée par Patzig, op. cit., p. 191, n. 1. ↵

36. Ὧι γὰρ ἄν τινὶ μὴ ὑπάρχῃ τὸ μὲσον, τούτῳ καὶ παντὶ καὶ οὐδενὶ ἀκολουθήσει τὸ πρῶτον. Sur le sens de ἀκολουθήσει, cf. la pertinente remarque de Patzig. op. cit., p. 190, n. 2 et p. 30, n. 2. ↵

37. Cf. 26 a 5-6. ↵

38. Εἶτα καὶ ὧν μὴ κατηγορεῖται λευκῶν ὁ ἂνθρωπος, εἰλὴφθω κύκνος καὶ χιών. Il est clair qu’à la place de ces concepts ‘naturels’ , Aristote aurait pu, sur sa lancée, continuer à construire les concepts ‘artificiels’ (C. ~B. A) et (C. ~B. ~A.), dont cygne et neige ne sont que des sous-concepts. ↵

39. Οὐκοῦν τὸ ζῷον τοῦ μὲν παντὸς κατηγορεῖται, τοῦ δὲ οὐδενός, ὥστε οὐκ ἔσται συλλογισμός. ↵

40. En termes abstraits: A, (A. B. C), (A. B). En termes concrets, par exemple: animal, homme, mammifère. Rien n’empêche naturellement d’utiliser aussi une triade qui donnerait une mineure trop forte: en termes abstraits, A, (A. B), (A. ~B); en termes concrets, par exemple, animal, homme, cygne. ↵

41. En termes abstraits: A, (A. B), (~A. ~B). En termes concrets, par exemple: animal, homme, neige. ↵

42. Patzig, op. cit., p. 191-192. ↵

43. “‘Einige weisse Dinge’ ist ein anderer Begriff als ‘Weisses’; und der zweite Satz würde durch die Einsetzung die Form ‘Mensch kommt einigen weissen Dingen allgemein nicht zu’ erhalten” (Patzig, op. cit., p. 192). Souligné par l’auteur. ↵

44. 26 b 10-14. ↵

45. Par instances contrastées, cf. 26 a 2-9. ↵

46. Op. cit., p. 193-194. ↵

47. Sur ce point, Patzig commet, me semble-t-il, une erreur en écrivant à propos du passage qui nous occupe (p. 190): “Wegen dieser ‘Unbestimmtheit’ [l’indétermination de la particulière] ist es nun in einigen Fällen nicht möglich, zwei Begriffstripel der verlangten Art zu finden, die die Prämissen, z. B. ao der ersten Figur erfüllen, ohne auch ae zu erfüllen.” En réalité, la raison pour laquelle il est impossible de trouver des prémisses qui satisfassent a-o sans satisfaire aussi a-e n’est pas l’indétermination de la particulière, mais la contradiction inhérente à la conjonction AaB. BoC. ~BeC. AeC; et l’indétermination de la particulière n’est pas la raison de cette situation, mais au contraire la condition sous laquelle une triade satisfaisant a-o sera considérée comme satisfaisant aussi a-e. Autrement dit, si Aristote s’en était tenu à la doctrine de l’indétermination de la particulière, sans se laisser troubler par l’usage courant, il n’aurait pas éprouvé de difficultés pour mener à bien, dans le cas qui nous occupe, sa preuve par instances contrastées; nous le verrons plus en détail ci-dessous, et du reste Patzig le dit excellemment lui-même, p. 191 (“Diese Schwierigkeit würde durch den Hinweis sofort beseitigt, den Aristoteles später ja auch aufnimmt, dass BoC nicht bedeuten muss, dass auch BiC gilt; dass BoC vielmehr auch wabr ist, wenn BeC wahr ist. Dann kônnte man z. B. Lebwesen, Mensch, Schnee als Begriffe A, B, C, einsetzen, die sowohl AaB und BoC wie AeC erfüllen. Diesen Weg gehe Aristoteles aber hier noch nicht”). ↵

48. Ἐνδέχεται δὴ καὶ παντὶ καὶ μηδενὶ τῷ Ξ τὸ Ν ὑπάρχειν (15-16). ↵

49. En seconde figure, les termes sont donnés dans l’ordre: moyen M, majeur N, mineur X. ↵

50. En termes abstraits: A, (~A. ~B. C), [(A. B) ∪ (~A. B)]. La particulière est ici maximale: noir convient aussi à quelque animal. ↵

51. Τοῦ δὲ παντὶ ὑπάρχειν οὐκ ἔστι λαβεῖν, εἰ τὸ Μ τῷ Ξ τινὶ μὲν ὑπάρχει τινὶ δὲ μή (16-18) ↵

52. Démonstration plus directe chez Alexandre d’Aphrodise, in An. Pr. 87, 9-28: Mo₂X implique MiX, qui, couplé avec la première prémisse MeN, donne NoX par Festino; cette conclusion contredit NaX, relation qu’on voulait obtenir. ↵

53. Il aurait pris une première triade satisfaisant MeN et Mo₂X, par exemple bois, animal, blanc en termes abstraits A, (~A. B). [(A. C) ∪ (~A. C)]. Il aurait ensuite pris. dans les choses blanches qui ne sont pas de bois (~A. C), un concept de formule (~A. B. C), par exemple cygne, puis un concept de formule (~A. B. ~C), par exemple neige; et il aurait tenu les relations NaX et NeX pour satisfaites, l’une par cygne, l’autre par neige, au prix de la substitution illégitime décrite plus haut. ↵

54. Il suffisait de prendre une triade satisfaisant MeN. MeX, et donc afortiori MeN. Mo_IX; Aristote en avait une à une portée de la main, puisqu’il avait démontré la non-concluance de MeN. MeX, en 27 a 22-22, par instances contrastées. La triade satisfaisant NaX était ligne, animal, homme; en termes abstraits. (~A. ~B), A, (A. B). ↵

55. Οὕτω μὲν οὖν οὐκ ἐγχωρεῖ λαβεῖν ὅρους, ἐκ δὲ τοῦ ἀδιορίστου δεικτέον (20-21). Οὕτω ne peut avoir d’autre sens que “si l’on prend une particulière de type Mo₂X”. ↵

56. Il en est de même dans tous les autres cas énumérés ci-dessus, sauf (7). Cf. les rejets des couples e-l de deuxième figure (27 b 27-28: τοῦ δὲ παντὶ οὐκ ἔσται λαβεῖν διὰ τὴν αὐτὴν αἰτίαν ἤνπερ πρότερον, ἀλλ’ ἐκ τοῦ ἀδιορίστου δεικτέον) a-o de troisième figure (27 b 24-28: τοῦ δὲ μηδενὶ οὐκ ἔστι λαβεῖν ὅρους […] ἀλλ’ ὥσπερ ἐν τοῖς πρότερον ληπτέον. ἀδιορίστου γὰρ ὄντος τοῦ τινὶ μὴ ὑπάρχειν κτλ.) (29 a 3-6: τοῦ δ’ ὑπάρχειν οὐκ ἔστι λαβεῖν […] ἀλλ’ ἐκ τοῦ ἀδιορίστου δεικτέον). ↵

57. H. Maier, Die Syllogistik des Aristoteles, Tübingen, 1896-1900. t. II a, p. 85 (86), n. I: “Diese Beobachtung hätte nun die Möglichkeit gegeben, den ursprünglichen Beweis zu Ende zu führen. [...]. Offenbar schwebt dem Aristoteles ursprünglich dieser Beweisabschluss vor. Anstatt jedoch so fortzufahren, bricht er vielmehr den ursprünglichen Beweis ab. Die Erwägung, dass das part.-verneinende Urteil unbestimmten Charakter hat, erinnen ihn daran, dass sich aus dieser Eigenschaft ein selbständiger Beweis führen lässt. So setzt er völlig neu an, usw.” ↵

58. Lukasiewicz, op. cit., p. 71: “Aristotle, however, does not finish his proof in this way, because he sees another possibility.” ↵

59. T. Sugihara, art. cit.: “Conceming the following 6 moods it is impossible to prove by contrasted instances that there is no syllogism if the premiss is particular, while it is possible if the premiss is indefinite. [...] All these statements of Aristotle about the moods can’t be interpreted rightly, unless his ‘particular’ is bilateral, and ‘indefinite’ is unilateral.” ↵

60. G. Patzig, op. cit., p. 194: “Das Verfahren ἐκ τοῦ ἀδιορίστου [...] wendet er dort und nur dort an, wo [...] die ehen erörtete Schwierigkeit besteht, dass man für eins der beiden Begriffstripel keine Termini finden kann, die nicht auch die allgemeine Form der zweiten Prämisse erfüllen. Dass nun tatsächlich diese Schwierigkeit Aristoteles in solchen Fällen auf das beschriebene Gcsetz zurückgreifen lasst, geht aus dem Text an allen diesen Stellen hervor. Es genügt, den Beweis für die Unschlüssigkeit von eo in der zweiten Figur hierherzusetzen.” ↵

61. Toujours en conformité avec l’usage adopté par G. Patzig, je note la proposition contingente en préfixant la lettre M, l’apodictique en préfixant la lettre N; l’absence de lettre préfixée dénote l’assertorique. M dénote, conformément à la définition ‘forte’ de la contingence: ni nécessaire ni impossible. Nous n’aurons pas ici à envisager les complications nées de la concurrence de la définition ‘faible’ (non impossible). ↵

62. Οὐκ ἔσται συλλογισμός. Ὅροι τοῦ μὲν ὐπάρχειν λευκόν-ζῷον-χιών, τοῦ δὲ μὴ ὑπάρχειν λευκόν-ζῷον-πίττα. διὰ γὰρ τοῦ ἀδιορίστου ληπτέον τὴν ἀπόδειξιν (35 b 9-11) ↵

63. Celle-ci se présente sous une forme modifiée en syllogistique modale, le nombre des relations à exhiber entre les extrêmes étant multiplié par le nombre des modalités qui peuvent affecter ces relations: théoriquement, il faudrait donc exhiber six triades de concepts pour éliminer toutes les relations possibles. Aristote se contente cependant d’exhiber deux triades, dans lesquelles les relations entre les extrêmes sont universelles et apodictiques. Cette simplification est justifiée en 14. 33 b 3-17: en exhibant la relation NAaC, on exclut les conclusions négatives apodictique et assertorique, et la conclusion affirmative problématique (parce que le nécessaire n’est pas contingent); en exhibant la relation NAeC, on exclut les conclusions affirmatives apodictique et assertorique, et la conclusion négative problématique. ↵

64. En termes concrets, par exemple: blanc, animal, blanc-comme-neige. En termes abstraits: A, [(A. B) ∪ (~A. B)], [(A. B. C) ∪ (A. ~B. C)]. ↵

65. Par exemple en montrant que BiC, impliqué par la mineure maximale Bo_sC, se combine avec la majeure MAaB pour donner (par Darii avec majeure contingente et mineure assertorique, cf. 35 a 30-35) la conclusion MAiC, qui contredit la relation cherchée NAeC. ↵

66. En termes abstraits: A, [(A. B. ~C) ∪ (~A. B. ~C)], (A. ~B. C). ↵

67. En termes abstraits: (A. ~C), [(A. B. ~C) ∪ (~A. B. ~C)], (~A. ~B. C). ↵

68. Cette manière de procéder n’est indispensable, on l’a vu, que dans l’un des deux cas, celui de la relation NAeC. Si Aristote l’a adoptée dans les deux cas, c’est d’abord parce qu’il s’est contenté de reproduire les triades dont il s’était servi pour démontrer la non-concluance de MAaB. BeC (ct: 35 a 20-24); c’est aussi, sans doute, parce qu’il tenait à présenter deux triades contenant deux termes communs. Cette contrainte favorise l’évidence intuitive de la preuve par instances contrastées; mais elle n’appartient pas à l’essence de la preuve (ct: Patzig, op. cit., p. 196). Ce point est, avec l’usage de concepts ‘naturels’ , le seul sur lequel Aristote paraisse n’avoir pas pris l’exacte mesure de ce qu’il y avait d’essentiel et d’accessoire dans son procédé. ↵

69. Cf. note 56. ↵

70. Cf. par exemple la démonstration de non-concluance de MAeB. MAaC (17, 37 a 32 s.), couple de seconde figure dont le correspondant assertorique est le mode concluant Cesare. Cesare pouvait se réduire à Celarent par conversion de la majeure; mais l’universelle négative ne se convertit plus lorsqu’elle est contingente. Cesare pouvait aussi se démontrer par l’absurde; cette démonstration n’est plus possible avec des prémisses contingentes, pout lesquelles les lois d’incompatibilité des assertoriques ne sont plus valables (AeC est incompatible avec AaC, mais MAeC ne l’est pas avec MAaC). ↵

71. Cf. par exemple le rejet de NAaB. AeC → NBeC (10, 30 b 185.), couple de seconde figure dont le correspondant assertorique est le mode concluant Camestres. Aristote démontre successivement ce rejet (1) en réduisant ce mode, par conversion de la mineure, à un mode de première figure dont il a déjà démontré que la conclusion n’est pas apodictique; (2) par l’absurde; (3) par “production de termes concrets” (ὅρους ἐκθέμενον). Cette dernière démonstration consiste en l’exhibition d’une triade unique, sur laquelle il nous faudra d’ailleurs revenir (animal, homme, blanc), qui permet d’exclure la conclusion NBeC. Il est inutile de chercher une triade capable d’exclure la conclusion NBaC, cell-ci étant a fortiori exclue par la conclusion BeC de Camestres, et les prémisses ici envisagées étant plus fortes que celles de Camestres. ↵

72. Ross a baptisé de ce nom (op. cit., p. 298) l’ensemble des lois admises par Aristote sur la base du principe selon lequel, si un état de choses est contingent, sa négation l’est aussi. Ces lois sont les suivantes:

MAaB → MAeB

MAaB → MAoB

MAeB → MAaB

MAeB → MAiB

MAiB → MAoB

MAoB → MAiB

Il faut noter que des deux expressions MAaB et MAiB, aucune désormais n’implique l’autre. De même pour MAeB et MAoB. ↵

73. En effet, MBaC ↔ MBo₁C ↔ ~NBaC. ~NBo₁C; MBeC ↔ ~MBi₁C ↔ ~NBeC. ~NBi₁C. Les négations sont naturellement équivalentes aussi: ~MBaC ↔ ~MBo₁C ↔ ~NBaC ∨ NBo₁C; ~MBeC ↔ ~MBi₁C ↔ NBeC ∨ NBi₁C. ↵

74. Cf. note 7O. ↵

75. Διὰ τῶν ὅρων (37 b 1-2). ↵

76. Par exemple, après avoir démontré grâce à une triade unique (blanc, homme, cheval, cf. ci-dessus paragraphe 3) la non-concluance de Me-Ma en seconde figure, Aristote ajoute: La démonstration sera la même si la négative est transposée [Ma-Me], si les prémisses sont toutes deux affirmatives [Ma-Ma] ou négatives [Me-Me] (la démonstration se fera en effet par les mêmes termes concrets, διὰ τῶν αὐτῶν ὅρων); de même lorsque l’une est universelle et l’autre particulière [Ma-Mi, Ma-Mo, Me-Mi, Me-Mo, Mi-Ma, Mi-Me, Mo-Ma, Mo-Me] ou toutes deux particulières [Mi-Mi, Mi-Mo, Mo-Mi, Mo-Mo] ou indéfinies, ou de toutes les autres façons qu’on pourra prendre les prémisses; la démonstration se fera toujours, en effet, par les mêmes termes concrets, ἀεὶ γὰρ ἔσται διὰ τῶν αὐτῶν ὅρων ἡ ἀπόδειξις (37 b 10-16). Aristote suppose que, puisqu’en fait quelques hommes sont blancs et quelques hommes ne sont pas blancs, aucune des quatre relations a, e, i, o n’est nécessaire entre les termes blanc et homme, et que ces termes satisfont donc les quatre relations Ma, Me, Mi, Mo, qui figurent toutes quatre dans les majeures des couples énumérés ici. ↵

77. Cf. note 71. ↵

78. Ἐνδέχεται γὰρ τὸ ζῷον μηδενὶ λευκῷ ὐπάρχειν (30 b 35). ↵

79. Signalons une conséquence de cet élargissement. S’il n’est plus nécessaire, pour éliminer une conclusion syllogistique, de signaler l’existence dans le monde réel de trois termes A, B, C qui l’infirment, et s’il suffit de signaler l’existence de tels termes dans un monde possible, il en résulte a contrario que les variables des conclusions syllogistiques valides sont substituables par des êtres possibles comme par des êtres réels. ↵

80. Οἱ γὰρ αὐτοὶ ὅροι ἔσονται πρὸς τὴν ἀπόδειξιν οἵπερ ἐπὶ τῶν καθόλου συλλογισμῶν (31 a 14-15). ↵

81. De Part. Anim. I 1, 642 a 27-28; cf. Metaph. A3, 984 a 18; Phys. I 5, 188 b 27. ↵

82. Au moment où je corrige les épreuves de cet article, je prends connaissance du livre récent de Lynn E. Rose, Aristotle’s Syllogistic, Springfield, Thomas, 1968, qui traite avec précision les problèmes que j’ai examinés, en particulier dans ses chapitres VI (‘Invalidation by counterexample’) et IX (‘Subalternation’). Je disais ci-dessus (n. 34) que les occurrences de la preuve par l’indéterminé n’avaient jamais été exhaustivement et systématiquement examinées. Ce n’est plus vrai: M. Rose en donne la même liste que moi, p. 40 de son livre. Il étudie en détailles cas 3, 1 et 7 dans son chapitre VI (p. 40-49), et le cas 5 dans son chapitre IX (p. 86-88, où l’on notera cependant qu’il se borne à recopier, avec les quelques transpositions nécessaires, ce qu’il avait dit p. 41-43 sur le cas 3). Je suis heureux de constater entre ses analyses et les miennes, une convergence qui va parfois jusqu’à de surprenantes rencontres. Cependant, en première approximation et sous réserve d’une étude plus poussée, je marquerai un désaccord sur deux points. Tout d’abord, je crois que M. Rose ne tient pas un assez grand compte du travail de G. Patzig (qu’il connaît et cite à l’occasion): il néglige aussi bien la critique très précise que cet auteur a faite du procédé utilisé en 26 b 3-14 (cf. ci-dessus, n° 38-44) que la défense qu’il a présentée du caractère logique, au moins en droit, de la technique de rejet par exemples contrastés (cf. ci-dessus, n° 28-30). En second lieu, M. Rose étudie les diverses procédures adoptées par Aristote dans un ordre arbitraire; elles apparaissent comme des tentatives un peu désordonnées pour sortir d’une situation difficile; l’originalité du cas 7. entrevue p. 49, n’est pas vraiment dégagée. J’ai essayé de montrer au contraire que ces procédures s’ordonnaient selon une ligne précise, manifestaient une prise de conscience progressive des données du problème et des conditions de sa solution, et permettaient d’assister, en quelque sorte, au travail de la formalisation. ↵