Sur le système des connecteurs interpropositionnels
1
[131]Lorsque la combinatoire, succédant à ce relevé purement empirique que suggéraient les usages linguistiques, eut dressé la table des seize connecteurs binaires que comporte nécessairement le calcul des propositions fondé sur les fonctions de vérité, on s’est naturellement soucié de reconnaître entre ces divers connecteurs certaines parentés, qui permissent, en raison des groupements qu’elles dégagent, d’introduire dans la table un commencement d’organisation.
On peut d’abord procéder d’une manière formelle et quasi mécanique, en se fondant sur le fait que les divers connecteurs sont
interdéfinissables avec le secours de la seule négation. On voit alors qu’à partir de l’un quelconque des seize connecteurs
théoriques entre deux propositions p et q – et pour ne considérer que celles des définitions qui ne comptent qu’une seule occurrence de p et de q – on peut d’abord en obtenir trois autres en faisant porter la négation soit sur p, soit sur q, soit sur les deux à la fois: par exemple à partir de p ∨ q on aura ¬p ∨ q(≡ p ⊃ q), p ∨ ¬q(≡ p ⊂ q), ¬p ∨ ¬q(≡ p │ q)i; puis, en affectant chacune de ces quatre formules d’une négation globale, on doublera la liste, obtenant ainsi un ensemble
de huit connecteurs. Telle est la procédure adoptée par K. Döhmann dans une récente étude1. Mais en agissant ainsi sur chacun des seize connecteurs pris comme origine, on s’aperçoit aussitôt que dans la moitié des
cas les huit formules ne donnent réellement que deux connecteurs, dont chacun a seulement reçu quatre formulations différentes
mais équivalentes, par exemple à partir de p 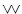 q : ¬p
q : ¬p 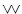 q (équivalent à p ≡ q), p
q (équivalent à p ≡ q), p 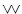 ¬q (id.), ¬p
¬q (id.), ¬p 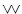 ¬q (équivalent à p
¬q (équivalent à p  q), etc. Et dans l’autre moitié, ce sont toujours les mêmes huit autres connecteurs, à savoir ceux des jonctions et ceux des
implications, qui reviennent, avec seulement, pour chacun des cas, un changement dans l’ordre.
q), etc. Et dans l’autre moitié, ce sont toujours les mêmes huit autres connecteurs, à savoir ceux des jonctions et ceux des
implications, qui reviennent, avec seulement, pour chacun des cas, un changement dans l’ordre.
Pareille systématisation nous parait passablement artificielle. Elle applique aveuglément un principe de diversification posé a priori, et dont le caractère relativement inadapté apparaît en ceci, que la matière lui oppose, dans la moitié des cas, une résistance. De plus, elle ne nous renseigne guère sur les rapports fonctionnels entre les divers connecteurs, qui sont tous mis sur le même plan. Nous pouvons néanmoins, au début de notre étude, en retenir deux leçons. La première, d’ailleurs parfaitement banale, est qu’à chaque connecteur on peut en associer un autre qui en est l’exacte négation, en ce que sa table permute, avec celle du premier, le vrai et le faux: ce qui permet d’assembler les seize connecteurs en huit couples. La seconde est la différence marquée qui se manifeste entre l’ensemble des jonctions et des implications d’une part et, d’autre part, celui des huit autres connecteurs. En d’autres termes, ce mode de systématisation nous met en présence de deux dichotomies distinctes, et qui se recoupent: celle qui oppose à chaque connecteur son négateur, et celle qui répartit les seize connecteurs en deux ensembles de huit dont l’un, dégénéré, nous ramène à quatre couples d’opposés contradictoires, tandis que l’autre présente une structure plus riche, dont Döhmann donne une analyse qui rejoint celle d’autres auteurs que nous allons rencontrer dans un instant. De ces analyses nous pourrons nous inspirer, mais seulement en les prenant comme un point de départ pour pousser plus avant. Car il subsiste des questions. Le sens de la première dichotomie est certes parfaitement clair, le rapport fonctionnel entre les deux membres de chaque couple d’opposés contradictoires étant celui, bien connu, de la négation mutuelle formant alternative. La seconde au contraire pose un problème: que signifie-t-elle, et comment ses termes s’articulent-ils entre eux d’un point de vue fonctionnel?
Après cette première manière d’associer deux connecteurs par la relation de négativité pour en faire des ‘couples d’opposés’ , un coup d’oeil jeté sur leur tableau fait apparaître une autre sorte de parenté entre certains connecteurs, à savoir ceux qui, exprimant une relation asymétrique, sont réversibles et comportent donc un converse. On trouve là un second principe de dualité. Entre ses deux membres, la dissymétrie se manifeste dans leurs tables et, plus immédiatement perceptible, dans leurs symboles, orientés dans deux sens opposés. Tel est le cas de l’implication, avec ses deux formes p ⊃ q et p ⊂ q. Comme chacun de ces deux connecteurs a son correspondant négatif, on peut, en combinant ces deux dualités, réunir en un groupe ces quatre connecteurs et former ainsi le ‘quaterne des implications’ , qu on pourra, pour plus de clarté intuitive, ordonner spatialement en un carré. Ainsi procède J. Piaget2, qui dispose diagonalement les couples des négations mutuelles, et situe sur chacun des deux côtés horizontaux les couples des converses, qu’il appelle – ayant réservé le mot d’ ‘inverses’ pour qualifier les négatives – des ‘réciproques’ . Maintenant, la combinaison de ces deux sortes de couples en une structure quadratique a pour effet d’appeler [133] un mode de couplage complémentaire, chacun des termes se trouvant mis en un certain rapport (symbolisé par les côtés verticaux du carré) avec celui qui est le réciproque de son inverse ou, ce qui revient au même, l’inverse de son réciproque; Piaget l’appelle son ‘corrélatif’ .
Enfin, une troisième façon d’accoupler des connecteurs est suggérée par une dualité remarquable, de portée très générale, et qui joue ici entre disjonction et conjonction. Les lois de De Morgan, en posant l’équivalence entre ¬(p ∨ q) et ¬p · ¬q ainsi qu’entre ¬(p · q) et ¬p ∨ ¬q, expriment cette correspondance entre les formules disjonctives et les formules conjonctives et permettent de les traduire commodément l’une dans l’autre. Si alors on associe à chacun de ces deux connecteurs sa négation, respectivement le rejet et l’incompatibilité, on obtient un second quaterne, le ‘quaterne des jonctions’ . Ainsi W. H. Gottschalk3 analyse un système quaternaire assez semblable à celui de Piaget, mais qui s’en distingue essentiellement en ce que le principe générateur qui s’y combine avec celui de la négativité est celui de la dualité morganienne, et non plus celui de la réciprocité des converses. Ce sont maintenant les côtés verticaux du carré, porteurs de cette relation de dualité, qui le déterminent. Restent alors à considérer les relations symbolisées par les horizontales, c’est-à-dire les duales des négatives, ou négatives des duales: Gottschalk les appelle les ‘contreduales’ . La figure ci-dessous, où est mise en pointillé la relation qui complète le carré, permet la comparaison entre les deux structures:
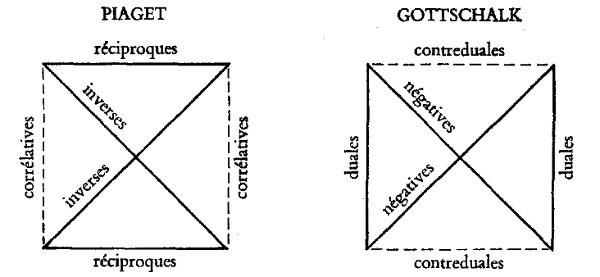
Seulement, ni Piaget ni Gottschalk ne limitent cette structure au cas typique que, si l’on en juge par leur vocabulaire, ils avaient apparemment dans l’esprit et qui, en tout cas, est celui auquel s’adapte le plus exactement leur schéma. Gottschalk, procédant en mathématicien, présente d’abord une théorie générale et abstraite de la quaternalité; il l’illustre ensuite par divers ‘modèles’ que comporte cette structure, entre autres ceux qu on peut construire à l’aide des tables de vérité du calcul des propositions; mais pour ceux-ci, en symbolisant par la lettre Φ, installée4 aux quatre coins [134] de son carré, un connecteur quelconque de ce calcul, il laisse entendre que son diagramme peut se tracer à partir de n’importe lequel d’entre eux. Piaget va en sens inverse: partant d’un examen des connecteurs5, c’est au terme de son analyse qu’il reconnaît qu’il a eu affaire au groupe quadratique de Klein6; Mais c’est expressément qu’il a appliqué, lui, cette structure à l’ensemble des seize connecteurs. Il les répartit en effet en quatre quaternes, quitte à admettre que deux d’entre eux présentent des formes dégénérées.
2
Ces théories, aux résultats convergents, sont précieuses à qui se propose d’organiser les connecteurs en une structure d’ensemble, et sans doute sont-elles, pour ce travail, une étape nécessaire. On ne peut cependant s’en tenir là, ni même les admettre sans retouches. Elles ne sont pas seulement incomplètes, ne nous apprenant rien sur la façon dont se comportent entre eux les divers quaternes; elles souffrent aussi de quelques assimilations sommaires, que refuse une analyse plus fine; enfin elles ne sont même pas toujours exemptes, quand on les pousse dans leurs détails, de ce qu’il faut bien regarder comme des inexactitudes.
On est d’abord frappé du nombre des connecteurs – exactement la moitié – qui échappent à cette structure quadratique, ou du moins qui ne s’y soumettent que par violence, puisque seuls s’y prêtent naturellement le groupe des jonctions et celui des implications. A ces connecteurs rebelles, Gottschalk fait à peine allusion: il pouvait en effet, ou plutôt il devait, son propos étant autre, laisser de côté ce qui ne s’accordait pas à la théorie de la quaternalité qui faisait l’objet de son article. Piaget au contraire, faisant porter son étude sur le calcul des propositions abordé par le biais des fonctions de vérité, était naturellement amené à s’occuper de ces connecteurs. Mais il veut les adapter de force à sa structure quadratique et il y parvient sans doute, mais avec quelque hésitation, semble-t-il, entre deux manières différentes, l’une et l’autre assez artificielles, et qui, par surcroît, s’accordent mal entre elles. Il commence par répartir ces huit connecteurs qui lui restent en quatre couples, en associant chacun à son ‘inverse’ , c’est-à-dire à sa négation. De ce point de vue, chacun de ces couples peut être regardé comme un quaterne dégénéré: soit que, comme c’est le cas pour tautologie-contradiction et pour équivalence-alternative, ses deux termes, parfaitement symétriques, soient à eux-mêmes leur propre réciproque de sorte que, la ligne horizontale s’évanouissant par télescopage, le carré s’amincit jusqu’à se réduire à une simple ligne verticale où les corrélatifs se confondent avec les inverses; soit que, comme c’est le cas pour les deux derniers couples, [135] chacun des termes soit son propre corrélatif, de sorte que cette fois le carré s’aplatit, par contraction complète de la ligne verticale, et se réduit à une simple ligne horizontale, celle des réciproques sur laquelle s’est rabattue pour s’y confondre la ligne des inverses. C’est ingénieux et acceptable. Mais aussitôt l’auteur s’engage dans une autre voie. Il assemble maintenant ces couples deux par deux, en vertu des analogies que nous venons d’indiquer; et cela, certes, est encore légitime. Seulement, il conserve le mot de ‘quaterne’ pour désigner chacun de ces deux assemblages. Et il hésite à nouveau: tantôt (quaterne C) juxtaposant en un seul quaterne deux de ces couples dont chacun apparaissait d abord comme étant lui-même un quaterne dégénéré, tantôt (quaterne D) disposant les deux couples selon la forme quadratique, alors que les relations caractéristiques qu’on avait d’abord attachées à cette forme sont ici complètement bouleversées. Dans un cas comme dans l’autre, il est clair que le mot de quaterne est pris maintenant dans une acception beaucoup plus vague, qui ne dépasse guère la notion d’un quatuor d’éléments plus ou moins apparentés. Il avait d’abord désigné un ‘être mathématique’ doué d’une structure bien déterminée, la structure quadratique de Klein sur laquelle se rencontrent les analyses de Piaget, de Gottschalk et de Döhmann, structure qui permet d’ordonner, comme Piaget venait lui-même de le faire, la famille des jonctions et celle des implications. Mais le mot est entendu maintenant au sens d’une simple ‘classe logique’ , qu’on forme en vertu de certaines ressemblances que présentent des éléments, dont il se trouve qu’ils sont au nombre de quatre, préalablement répartis en deux couples.
3
C’est donc dans une autre voie qu’il faut s’engager7 pour poursuivre la structuration du tableau des seize connecteurs binaires, c’est-à-dire d’une part pour rattacher les quatre couples d’antithétiques aux deux quaternes fermement construits, d autre part pour déterminer exactement le rapport entre ces deux derniers.
Nous pourrons d’abord simplifier le premier de ces problèmes en négligeant systématiquement les deux couples que Piaget a ressemblés dans son quaterne D, à savoir l’affirmation ou la négation de p ou de q. Ceux-là sont incontestablement des binaires dégénérés, retombés au niveau des foncteurs singulaires. Ils ne figurent dans le tableau des connecteurs binaires que pour des raisons de pure combinatoire puisque, portant sur une seule proposition, ils ne sont réellement ni des binaires ni, partant, des connecteurs. On ne peut les ranger parmi les binaires qu’au sens où l’on rangerait parmi les duos [136] une partition où l’un des deux ‘exécutants’ demeurerait constamment silencieux. De fait, ils ne servent à rien, et les logiciens n’ont pas éprouvé le besoin de leur assigner un symbole. Pourquoi en effet faire appel à une forme inutilement compliquée, puisqu’on peut exprimer la même chose en écrivant simplement p, ou q, ou ¬p, ou ¬q? N’ayons donc aucun scrupule à les laisser de côté.
Nous ne pouvons pas en user de même avec les deux autres couples, tautologie-contradiction, équivalence-alternative, lesquels jouent un rôle essentiel dans le calcul. Mais il faut se garder, non seulement de les grouper en un quaterne, mais même de les assembler en une même classe. Si l’on peut être tenté de le faire en raison de certaines analogies, on masque ainsi ce fait capital, que le couple tautologie-contradiction diffère totalement, par ses fonctions, non seulement du couple équivalence-alternative, mais de l’ensemble des autres connecteurs; de sorte qu’il faut lui ménager, parmi ceux-ci, une place tout à fait à part, comme c’est d’ailleurs très généralement reconnu.
D’abord parce que la tautologie et la contradiction ne sont pas essentiellement, comme sont l’équivalence et l’alternative,
des binaires. On pourrait sous ce rapport, comme fait Parry8, les joindre aux quatre dégénérés pour dire que ces six prétendus binaires sont en réalité assimilables à des singulaires, dont la table les retrouve à ses deux extrémités; mais on dirait aussi bien
qu’ils sont des ternaires, ou plus généralement des n-aires, puisque, de toute façon, ils déterminent les deux limites extrêmes de la table. Faut-il même les regarder comme de
vrais connecteurs? On ne peut les ranger parmi ceux-ci que selon ce genre de convention par laquelle le mathématicien s’autorise à inclure
dans un ensemble les termes qui forment ses frontières, par exemple à traiter zéro comme un entier, à regarder un segment
de droite comme un angle de 0° ou de 360°, etc. La vérité d’une formule tautologique, ou la fausseté d’une formule contradictoire, n’est pas proprement fonction de
celle des propositions élémentaires qui la composent, puisqu’elle ne varie pas en fonction de celle-ci; ou alors disons seulement,
en un sens élargi, que tautologie et contradiction “sont des fonctions dont la valeur est constante”9. Mais quel que soit le choix du vocabulaire, il reste qu’une différence fondamentale sépare ces
‘foncteurs’
, ces
‘connecteurs’
, ces
‘opérateurs’
, de tous les autres. L’écriture symbolique manifeste cette différence. On n’écrit pas p T q comme on écrit, par exemple, p ≡ q ou p 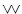 q, p ∨ q ou p ⊃ q; on dit, dans la métalangue, qu’une formule telle que, par exemple, p ⊃ q · ≡ · ¬p ∨ q est tautologique; ou bien on la fait précéder du symbole métalinguistique d’assertion, lequel porte d’ailleurs sur l’ensemble
de la formule et ne joue [137] donc pas proprement le rôle d’un connecteur; il porte sur le connecteur principal de la formule, pour marquer que celui-ci
prend une valeur apodictique. Reichenbach peut donc écrire, en un sens parfaitement acceptable, que “ces deux cas extrêmes ne définissent pas des opérations” – en tout cas, pas des opérations dans le même sens que les autres – de sorte que si l’on retranche en outre les quatre cas
de dégénérescence, il ne subsiste plus réellement que dix opérations10, les seules, en fait, à avoir leur symbole.
q, p ∨ q ou p ⊃ q; on dit, dans la métalangue, qu’une formule telle que, par exemple, p ⊃ q · ≡ · ¬p ∨ q est tautologique; ou bien on la fait précéder du symbole métalinguistique d’assertion, lequel porte d’ailleurs sur l’ensemble
de la formule et ne joue [137] donc pas proprement le rôle d’un connecteur; il porte sur le connecteur principal de la formule, pour marquer que celui-ci
prend une valeur apodictique. Reichenbach peut donc écrire, en un sens parfaitement acceptable, que “ces deux cas extrêmes ne définissent pas des opérations” – en tout cas, pas des opérations dans le même sens que les autres – de sorte que si l’on retranche en outre les quatre cas
de dégénérescence, il ne subsiste plus réellement que dix opérations10, les seules, en fait, à avoir leur symbole.
Plutôt que deux opérateurs ou connecteurs particuliers, il est donc plus exact, d’un point de vue fonctionnel, de regarder la tautologie et la contradiction, à la manière de Serrus dont se moque Piaget11, comme des sortes de matrices desquelles s’obtiennent les véritables connecteurs. On pourra le voir commodément avec la disposition suivante. Écrivons sur une première ligne la forme normale disjonctive de la tautologie; puis, en dessous, en une seconde ligne, les négations de chacun des quatre éléments de la première, c’est-à-dire la forme normale disjonctive de la contradiction, en en modifiant seulement l’ordre usuel de façon que tous les couples de négations mutuelles soient disposés en obliques, déterminant ainsi comme deux carrés. On constate alors que le groupe des quatre éléments de gauche forme le carré des jonctions, et que celui des quatre éléments de droite forme le carré des implications, exprimé naturellement ici en langage de jonctions12:
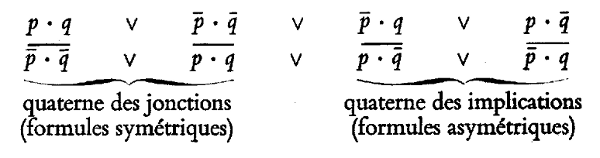
Si maintenant, dans la première ligne ci-dessus, on prend le premier couple, on s’aperçoit que cette disjonction donne l’équivalence
p ≡ q, et si l’on prend le second, qu’elle donne l’alternative p 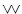 q. On retrouverait ce même couple si l’on opérait sur la seconde ligne, mais cette fois en conjoignant, au lieu de les disjoindre13, les deux termes de chaque couple, la première de ces conjonctions donnant l’alternative, la seconde donnant l’équivalence.
On obtiendrait naturellement des résultats analogues, mutatis mutandis, si l’on partait des formes normales conjonctives de la tautologie et de la contradiction. C’est là une première façon, encore
un peu sommaire, de marquer les relations essentielles des deux véritables connecteurs binaires, en les dégageant de leur
matrice commune.
q. On retrouverait ce même couple si l’on opérait sur la seconde ligne, mais cette fois en conjoignant, au lieu de les disjoindre13, les deux termes de chaque couple, la première de ces conjonctions donnant l’alternative, la seconde donnant l’équivalence.
On obtiendrait naturellement des résultats analogues, mutatis mutandis, si l’on partait des formes normales conjonctives de la tautologie et de la contradiction. C’est là une première façon, encore
un peu sommaire, de marquer les relations essentielles des deux véritables connecteurs binaires, en les dégageant de leur
matrice commune.
4
Considérons maintenant de plus près la structure quaternaire qui est commune, aux termes près, aux théories de Piaget et de Gottschalk, et qui ne s’adapte exactement qu’au cas des jonctions et des implications. Il est d’abord assez manifeste que, pour isomorphes qu’ils soient, les deux quaternes ne résultent pas du même mode de construction, ainsi que nous l’avons noté dès le départ, et comme le fait apparaître la comparaison de nos deux schémas du §1. Seule leur est commune la relation des inverses-négatives, laquelle, en dehors d’eux, joue d’une façon générale pour l’ensemble des connecteurs. En revanche, la relation de réciprocité ne joue proprement qu’entre des connecteurs asymétriques comme sont les implications, et ne peut donc être étendue au cas des jonctions que par un élargissement forcé du sens du mot: car pour des connecteurs symétriques, le renversement de la relation ou de son symbole, ou, ce qui revient au même, la permutation de ses termes, est une opération identique qui ne saurait, comme telle, fournir un principe de dualité. La dualité morganienne, d’autre part, joue essentiellement entre des jonctions, et ne s’étend ensuite aux implications que parce que celles-ci se laissent traduire en jonctions. Dans chacun des deux quaternes, le troisième mode de couplage apparaît alors comme dérivé. Les ‘corrélatives’ , dont le nom même est peu expressif, ce sont simplement les inverses des réciproques qui sont aussi bien les réciproques des inverses; et des ‘contreduales’ on dirait également que leur nom est peu expressif, si ce n’est qu’il exprime précisément, par rapport aux ‘duales’ , leur caractère dérivé.
N’insistons pas cependant sur cette différence dans le principe de formation des deux quaternes, puisqu’elle n’affecte guère, du moins à première inspection, la structure des deux carrés une fois formés. Mais, une fois ainsi admise leur assimilation d’un point de vue formel, demandons-nous plutôt si, d’un point de vue formel même, cette structure a bien été, chez nos deux auteurs, suffisamment analysée et si, telle qu’ils la présentent, elle ne souffre pas d’imperfections assez graves. L’un et l’autre se trouvent naturellement amenés, dans la suite de leur analyse, à rapprocher ce quaterne, avec la disposition quadratique qu’ils lui donnent, du classique carré des propositions opposées. Rapprochement parfaitement justifié, mais qui aurait dû mettre en éveil et suggérer de rectifier, en la précisant, la présentation primitive du quaterne. Car une différence saute aussitôt aux yeux: le carré des opposées a un haut et un bas, marqués par la distinction des contraires et des subcontraires, et par la direction de la subalternation; tandis que celui des connecteurs tolère qu’on le renverse: qu’on regarde son reflet dans un miroir, rien n’est changé à la disposition de ses relations constitutives. Dès lors, de deux choses l’une: ou bien l’analogie formelle entre les quaternes des connecteurs et le carré des propositions opposées n’est que superficielle et partielle, et le rapprochement n’en doit être fait qu’avec certaines réserves; ou bien les [139] deux systèmes sont réellement isomorphes, et alors il faut retoucher l’esquisse qu’on avait faite du quaterne des connecteurs. Dans les deux cas, par conséquent, des précautions s’imposent. Or, un examen plus attentif révèle que c’est le second membre du dilemme qui est le bon, et qu’il faut donc apporter certaines corrections à la présentation des quaternes.
Si en effet l’on construit d’abord ceux-ci sans se soucier de l’analogie avec le carré des opposées, peu importe qu’on situe le connecteur originaire, conjonction ou implication directe, sur la ligne du haut ou sur celle du bas; on préférera sans doute, en raison précisément de son caractère originaire, le situer en haut; en tout cas, et quelle que soit la ligne choisie, on jugera plus indiqué, pour souligner l’analogie qu’on professe entre les deux quaternes, de situer ces deux connecteurs en des positions homologues, et donc sur la même ligne. Seulement, si l’on en vient ensuite à amener en coïncidence ce schéma quadratique ainsi unifié et traité comme arbitrairement réversible, avec le carré traditionnel des opposées, dont la structure comporte une différenciation selon la verticale, on s’expose à des mécomptes.
Premièrement, le carré des opposées fait une différence entre d’une part les contraires qui, ne souffrant pas d’être vraies ensemble mais pouvant être toutes les deux fausses, se comportent comme des incompatibles, et d’autre part les subcontraires qui, ne souffrant pas d’être fausses ensemble mais pouvant être toutes les deux vraies, se comportent comme des disjointes. Or il est facile de s’apercevoir que cette même différence se retrouve dans les quaternes des connecteurs, ce qui supprime toute liberté pour la place où situer la cellule génératrice. La conjonction entre deux propositions et leur commun rejet sont incompatibles, de même que les deux non-implications entre ces deux propositions; tandis que leur disjonction et leur incompatibilité sont simplement disjointes, de même que les deux implications. La relation horizontale de contredualité-réciprocité doit donc être nuancée, il faut la dédoubler entre contreduales et subcontreduales; ou, selon l’autre vocabulaire, entre réciproques et subréciproques.
Deuxième différence, liée à la précédente: le carré logique distingue entre subalternante et subalternée, la première impliquant
la seconde, sans réciprocité. Autre raison pour distinguer de même entre le haut et le bas des quaternes, pour ne pas regarder
comme permutables les deux termes des duales-corrélatives, donc pour introduire une dissymétrie dans la relation verticale
qui les unit, en la marquant d’une flèche qui pointe vers le bas, bref pour donner aux quaternes une tête et des pieds, et
veiller à ne pas les faire reposer sur la tête. Car la relation asymétrique d’implication joue bien dans les deux quaternes,
comme il est facile de le vérifier par le calcul ou même par un simple examen des tables de vérité: p · q · ⊃ · p ∨ q, p ∧ q · ⊃ · p │ q, et de même p 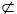 q · ⊃ · p ⊃ q, p
q · ⊃ · p ⊃ q, p 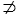 q · ⊃ · p ⊂ q, sans réciprocité.
q · ⊃ · p ⊂ q, sans réciprocité.
Il importe ici de ne pas faire une confusion entre la relation de dualité entre deux connecteurs, qui est symétrique et donc réciproque, en ce sens que la duale de chacun des deux, par exemple conjonction et disjonction [140] – disons plus exactement conjoncteur et disjoncteur – a l’autre pour sa propre duale, de sorte que si ¬(p ∨ q) ≡ · ¬p · ¬q, alors ¬(p · q) ≡ · ¬p ∨ ¬q et réciproquement – et la relation logique entre les deux formules dont chacune a pour connecteur celui qui est en dualité avec l’autre, par exemple la formule conjonctive p · q et la formule disjonctive p ∨ q, lesquelles n’ont pas même force logique, de sorte que la première implique bien la seconde, mais non inversement.
On verra alors, comme notre tableau du §3 pouvait le laisser soupçonner, que la cellule originaire de chacun des quaternes ne doit pas être située sur la même ligne: la conjonction doit prendre place à la ligne supérieure, puisqu’elle est subalternante ou implicante par rapport à la disjonction, et contraire ou incompatible par rapport au rejet; tandis que l’implication doit être située à la ligne inférieure, puisqu’elle est subalternée ou impliquée par rapport à la non-implication converse, et qu’elle est subcontraire ou disjointe par rapport à sa propre converse. La raison de cette différence doit être cherchée dans le fait que l’implication, admettant trois cas de vérité, demeure relativement indéterminée quant au vrai, l’un de ses trois cas incluant le cas unique de vérité de la non-implication converse: il est donc impliqué par elle, sans réciprocité. Et de même pour la disjonction et l’incompatibilité. C’est cette indétermination qui oblige à situer tant les deux implications que la disjonction et l’incompatibilité à la place qu’occupent, dans le carré logique, ces indéterminées que sont les particulières. Tandis que sur la ligne supérieure doivent figurer les connecteurs qui sont déterminés au maximum quant au vrai, ne comptant chacun qu’un unique cas de vérité. Un raisonnement analogue expliquerait, pour les connecteurs comme pour les propositions quantifiées classiques, la différence entre le cas des contraires, dont l’unique cas de vérité ne peut coïncider tandis que le peuvent deux de leurs cas de fausseté, et celui des subcontraires, pour lesquels c’est l’inverse. Et l’on comprend, du même coup, pourquoi nous ne pouvons, avec nos seize connecteurs, former que deux quaternes: seuls se prêtent à cette structure quaternaire ceux des connecteurs qui comptent un nombre impair de cas de vérité et de fausseté – ou, ce qui revient au même, ceux qui ont des formes normales impaires: c’est-à-dire exactement la moitié d’entre eux.
5
Dans cette différence de situation, à l’intérieur de chacun de nos deux quaternes, de son élément originaire, conjonction ou implication, on trouvera sans doute une nouvelle raison, s’ajoutant à celle que nous donnions au début, pour se garder de pousser trop loin leur assimilation mutuelle. D’autres raisons interviennent encore qui invitent, non seulement à reconnaître chacun dans son originalité propre, mais à établir entre eux une hiérarchie, ainsi que déjà le suggérait le fait que, des deux connecteurs qui [141] les commandent, c’est la conjonction, non l’implication, qui occupe dans le carré ce qu’on pourrait appeler la place noble, puisqu’elle l’emporte sur l’autre en force et en détermination.
Dans le calcul classique des propositions, les divers ‘connecteurs’ n’établissent pas, entre les deux propositions qu’ils mettent en rapport, une vraie connexion. Ils n’ont, comme dit Reichenbach, qu’une fonction purement adjonctive. L’implication, notamment, ne marque nullement, comme son nom le suggère faussement aux esprits non prévenus, un lien de dépendance entre deux propositions, plus ou moins apparenté à celui de principe à conséquence. Dire que p implique q, c’est simplement dire qu’on n’a pas à la fois p et non-q, ou encore qu on a non-p ou q, bref c’est énoncer une conjonction ou une disjonction, qui ne diffèrent de la conjonction p · q et de la disjonction p ∨ q qu’en ce qu’elles font intervenir une négation qui, portant sur l’une des deux propositions, donne à la formule l’asymétrie que ne pouvait porter le connecteur jonctif et que requiert l’implication: ¬(p · ¬q), ou ¬p ∨ q. L’implication, c’est une jonction avec asymétrie quant à l’affirmation et à la négation de ses deux propositions: c’est-à-dire, en somme, une forme de jonction plus complexe, dérivée d’une jonction qu’on peut bien regarder comme plus élémentaire, puisqu’elle ne présente pas encore cette complication qu’y introduira la dissymétrie entre ses deux membres. C’est pourquoi on a proposé, pour éviter le piège tendu par le vocabulaire, de la qualifier d’ ‘implication adjonctive’ (Reichenbach) ou même de la ramener expressément à une espèce particulière de jonction, en qualifiant celle-ci de ‘philonienne’ (W. Kneale). En fait, les logiciens ont bien senti cet ordre de dérivation, puisque, tout en professant qu’on peut, à l’aide de la négation, définir tous les connecteurs à partir de l’un quelconque d’entre eux, ils ont eu le plus souvent tendance à choisir l’une des jonctions comme notion première, et à définir par elle l’implication, comme c’est le cas pour les deux grands traités fondamentaux de logique moderne, les Principia mathematica de Whitehead et Russell et les Grundzüge der theoretischen Logik de Hilbert et Ackermann. Et de même, les ‘formes normales’ des seize connecteurs sont présentées par Hilbert comme des conjonctions de disjonctions ou des disjonctions de conjonctions.
Il est vrai qu’on pourrait être tenté de renverser l’argument, et de dire: puisque les divers connecteurs sont interdéfinissables, cela nous interdit de privilégier tel ou tel d’entre eux, et nous pouvons aussi bien, si nous le voulons, dériver les jonctions des implications, ainsi que l’ont fait réellement certains logiciens comme Frege et Lukasiewicz. Et de même, il est possible de construire des formes normales implicatives14. A pareille objection, nous pourrions d’abord répondre qu entre diverses constructions également correctes du point de vue logique, la raison peut inviter, pour des motifs de simplicité, de symétrie, de naturel, de genèse effective, etc., à préférer l’une d’entre elles; et nous venons de dire pourquoi, à cet [142] égard, le caractère purement adjonctif des connecteurs invitait à leur donner pour principes les adjonctions les plus simples, c’est-à-dire, en tout premier lieu, la conjonction. Mais puisqu’une telle réponse ne saurait satisfaire un pur formaliste, plaçons-nous donc nous aussi sur son terrain. L’objection que nous examinons repose sur la thèse classique de l’interdéfinissabilité des seize connecteurs. Juste en gros, cette thèse appelle cependant un examen plus précis dans le cas qui nous occupe, celui de la traductibilité mutuelle entre jonctions et implications. S’il est exact que l’implication se laisse exactement définir, à l’aide de la négation, à partir de la conjonction ou de la disjonction, il n’en va plus tout à fait de même quand on veut procéder en sens inverse. Car si l’on définit la conjonction par ¬(p ⊃ ¬q), et la disjonction par ¬p ⊃ q, on laisse échapper une partie du défini, la conjonction comportant aussi le cas où ¬(q ⊃ ¬p), qui n’est pas équivalent à ¬(p ⊃ ¬q), et la disjonction le cas où ¬q ⊃ p, non équivalent à ¬p ⊃ q. Il faudrait, pour avoir ici une définition qui convienne à tout le défini, conjoindre ces deux éléments de la définition, c’est-à-dire faire déjà usage d’une jonction, et introduire ainsi le défini dans le définissant. Ou bien donc la définition demeurera incomplète, ou bien elle souffrira d’une faute grossière. A moins qu’on fasse appel à la métalangue, en se permettant alors de sortir du plan du calcul. En d’autres termes: on n’a pas le droit d’écrire, pour définir exactement p · q, la formule ¬(p ⊃ ¬q) · ¬(q ⊃ ¬p), mais seulement l’expression ¬(p ⊃ ¬q) et ¬(q ⊃ ¬p) en révélant par ce ‘et’ non symbolique qu’une jonction ne se laisse pas intégralement traduire, dans la langue du calcul, en termes combinés d’implication et de négation. L’interdéfinissabilité entre les divers connecteurs n’est donc pas parfaite, on doit admettre une certaine irréductibilité des jonctions par rapport aux implications, tandis que la réductibilité joue bien en sens inverse. Ainsi se marque, au niveau même du calcul classique, une certaine priorité logique des jonctions sur les implications.
6
Après avoir ainsi essayé de dégager, pour chacun des deux quaternes, ce qui fait son caractère propre, et de les situer l’un par rapport à l’autre dans leur ordre normal de dépendance, revenons maintenant à la structure commune qu’ils présentent une fois constitués, et poursuivons notre recherche d’une organisation systématique de l’ensemble des dix vrais connecteurs.
Le tableau du § 3 nous en avait déjà donné quelque idée. Il nous montrait en effet, d’abord que le couple équivalence-alternative surgissait naturellement dans l’un et l’autre quaterne, mais aussi qu’il y surgissait en des places différentes, avec une sorte de croisement: l’équivalence s’obtenant, avec les jonctions, par la disjonction p · q · ∨ · p ∧ q des deux membres de la ligne supérieure, tandis qu’elle s obtient, avec les implications, [143] par la conjonction p ⊃ q · p ⊂ q des deux membres de la ligne inférieure; et inversement pour l’alternative. Ce qui suggérait déjà une certaine manière d’articuler, par la médiation de ce couple, les deux quaternes, et d’achever ainsi le système.
Mais l’analogie structurale que nous avons ensuite reconnue entre nos deux quaternes et le carré logique traditionnel, et qui nous a déjà permis de corriger leur première ébauche, va maintenant nous permettre aussi de préciser cette structure d’ensemble – à condition toutefois que l’on corrige à son tour, ou plutôt que l’on complète, le réseau des relations que soutient ce carré, en lui ajoutant deux postes supplémentaires qui le transforment en un hexagone. Ce n’est pas là une invention ad hoc, forgée arbitrairement tout exprès pour arriver à loger notre couple équivalence-alternative. La modification sortira renforcée de cette nouvelle application, mais elle était préalablement appelée, sans même parler des raisons de symétrie, par la seule considération des propositions opposées, où il convient d’introduire entre les deux particulières, pour se conformer aux usages les plus courants du langage et de la pensée, un “quelque” qui les conjoigne, signifiant “un au moins mais non pas tous”; et de même par la considération des quatre modalités aristotéliciennes, pour lever, par l’institution expresse d’une notion qui les conjoigne, l’ambiguïté permanente des notions du possible et du contingent, qui flottent l’un et l’autre entre le sens unilatéral où ils s’opposent comme des subcontraires, et le sens bilatéral où ils se confondent; etc. Ce qui appellera naturellement un sixième poste, pour être la négation contradictoire de celui-ci. Nous avons ailleurs longuement étudié cette structure hexadique, en analysant d’abord, d’un point de vue formel et abstrait, les diverses relations qui jouent entre ses six postes, et en en trouvant ensuite l’application en de multiples “modèles”. Pour poursuivre les désignations traditionnelles des différents postes du carré par les voyelles, nous avons désigné par Y ce poste intermédiaire entre I et O, dont il est la conjonction, et par U sa négation contradictoire, intermédiaire entre A et E dont il est la disjonction.
Or ce cadre hexagonal trouve ici une nouvelle occasion de s’appliquer. Dans le quaterne des jonctions, l’équivalence – disjonction de la conjonction et du rejet qui occupent respectivement les postes A et E – se situe en U, point culminant de l’hexagone, tandis que sa négation qui est l’alternative – conjonction de la disjonction et de l’incompatibilité qui occupent les postes I et O – se situe en Y, au point diamétralement opposé à U. Une même organisation hexadique est possible, selon les mêmes principes, pour les implications, mais en inversant les situations respectives de l’équivalence, qui tombe maintenant en Y, et de l’alternative, maintenant en U. Nous avons alors, par cette double parenté de chacun des deux termes du couple équivalence-alternative, le moyen d’unir les deux familles des jonctions et des implications, et de rassembler le tout en un système unitaire. On le représentera schématiquement par les hexagones ci-dessous, qui communiquent par les postes U et Y où se situent l’équivalence et l’alternative, [144] le poste U de l’un coïncidant avec le poste Y de l’autre, et réciproquement (les flèches marquent le sens dans lequel joue l’implication):
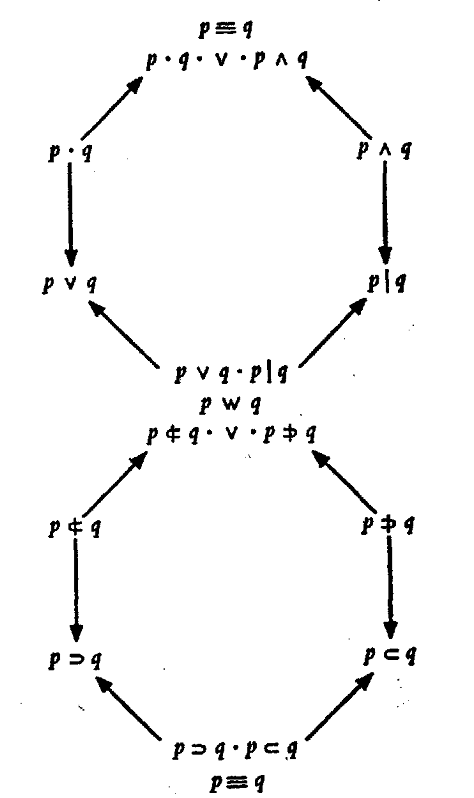
Il n’est certes pas toujours nécessaire de prendre en considération cette constellation totale, ni même la totalité de 1 un
de ses hexagones. Certaines familles usuelles de concepts laissent inoccupé, en fait, tel ou tel poste. Il est donc loisible
de les négliger éventuellement et de réduire ainsi la structure. On pourra notamment y retrouver, si l’on veut, le carré traditionnel.
Ou bien, si le système de notions qu’on analyse requiert une structure ternaire régulière, on isolera le triangle des contraires
AYE, en l’associant ou non à celui des subcontraires UIO qui en offre la réplique négative. Pour prendre un exemple, assurons-nous
que, dans chacun de nos deux quaternes, la triade des contraires vérifie bien les relations qui caractérisent cette triade
sur son schéma formel et abstrait. Nous l’appelons triade (ou triangle, sur sa représentation figurée) des contraires, parce qu’entre ses trois termes joue la relation d’incompatibilité, caractéristique de la contrariété: la position de l’un
de ses termes excluant celle des deux autres. Seulement, tandis que les deux contraires traditionnels A et E laissent échapper
le cas qu’elles excluent en commun, ce troisième cas est précisément celui que recueille le poste Y. Avec cette addition,
les contraires cessent de former un système [145] déficient, pour faire place à un système qu’on peut qualifier de parfait, en ce sens qu’il ne comporte ni redondance ni lacune,
que ses termes ne sont pas seulement mutuellement exclusifs, c’est-à-dire incompatibles entre eux, mais aussi collectivement
exhaustifs. La position de l’un quelconque de ses postes implique la négation des deux autres, puisque les trois sont incompatibles;
la négation conjointe de deux quelconques d’entre eux implique l’affirmation du troisième, puisque le système est complet.
Or on constate que ces relations jouent bien avec nos deux familles de connecteurs. Pour les implications, avec le triangle
p 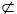 q, p ≡ q, p
q, p ≡ q, p 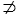 q. C’est en effet une thèse du calcul classique des propositions, liée à ce qu on appelle quelquefois les paradoxes de l’implication,
qu’entre deux propositions quelconques il y a toujours, d’une façon ou d’une autre, une relation d’implication. Dès lors,
ou bien cette relation est mutuelle, et alors il y a équivalence ou, comme on dit, double implication; ou bien l’une ou l’autre
des implications manque, et alors on a nécessairement soit p
q. C’est en effet une thèse du calcul classique des propositions, liée à ce qu on appelle quelquefois les paradoxes de l’implication,
qu’entre deux propositions quelconques il y a toujours, d’une façon ou d’une autre, une relation d’implication. Dès lors,
ou bien cette relation est mutuelle, et alors il y a équivalence ou, comme on dit, double implication; ou bien l’une ou l’autre
des implications manque, et alors on a nécessairement soit p 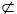 q, soit p
q, soit p 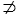 q: le système est complet. Et il n’est pas redondant, car les deux derniers cas sont évidemment incompatibles avec le premier,
et ils sont, d’autre part, en vertu de la thèse que nous venons de rappeler, incompatibles entre eux. De même pour les jonctions,
avec le triangle p · q, p
q: le système est complet. Et il n’est pas redondant, car les deux derniers cas sont évidemment incompatibles avec le premier,
et ils sont, d’autre part, en vertu de la thèse que nous venons de rappeler, incompatibles entre eux. De même pour les jonctions,
avec le triangle p · q, p 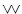 q, p ∧ q. Car s’il n’y a pas alternative entre deux propositions, c’est ou bien qu’elles sont toutes les deux vraies, p · q, ou bien qu’elles sont toutes les deux fausses, p ∧ q: le système est complet. Et il n’est pas redondant, les deux derniers cas étant évidemment incompatibles entre eux et chacun
d’eux excluant le premier et étant exclu par lui.
q, p ∧ q. Car s’il n’y a pas alternative entre deux propositions, c’est ou bien qu’elles sont toutes les deux vraies, p · q, ou bien qu’elles sont toutes les deux fausses, p ∧ q: le système est complet. Et il n’est pas redondant, les deux derniers cas étant évidemment incompatibles entre eux et chacun
d’eux excluant le premier et étant exclu par lui.
Ainsi viennent s’articuler entre eux les deux quaternes des connecteurs, chacun d’eux s’insérant dans une structure hexadique préalablement reconnue de façon indépendante et dont il apporte une nouvelle réalisation, puis communiquant avec l’autre par le couple qui leur est commun pour former une constellation décadique, celle-ci épuisant la liste des dix connecteurs qui, dans le calcul classique des propositions, sont proprement des opérateurs binaires.
7
Maintenant ce calcul classique lui-même, s’il fournit, par sa simplicité, une base nécessaire à toute étude des rapports logiques entre propositions, est loin de suffire à exprimer tous ceux que met en oeuvre la pensée même la plus banale. Il demeure sur le plan de la pure assertion, et écarte systématiquement de ses connecteurs toute nuance modale: c’est le sacrifice qu’il lui faut consentir, pour se prêter à un traitement vérifonctionnel. En quoi il fait souvent violence à nos modes les plus naturels de pensée, comme l’atteste, pour l’un comme pour l’autre de nos quaternes, le détournement de sens qu’il doit faire subir aux mots du vocabulaire. Car dans la langue commune, et aussi bien dans la langue littéraire, dire qu’une proposition [146] en implique une autre signifie que la seconde est une conséquence nécessaire de la première; et dire que deux propositions sont compatibles ou incompatibles signifie qu’il est ou non possible qu’elles soient vraies ensemble. Et on notera même que c’est seulement lorsqu’il y a, entre deux propositions, une implication ou une incompatibilité en ce sens fort, que nous parlons d’une relation logique entre elles. Car avec la logique nous sommes proprement, certains diront même exclusivement, dans le domaine de la nécessité. Tandis que, toujours avec le sens modal de ces termes, la non-implication, directe ou converse, et la simple compatibilité, sont précisément l’expression de l’absence de lien logique entre deux propositions.
Au système des connecteurs assertoriques, il convient donc de superposer, même au prix de difficultés pour un traitement formel,
un système de connecteurs modalisés, où soit observée avec le premier une correspondance terme à terme. Doubler donc l’implication
assertorique dite
‘matérielle’
par une implication apodictique dite
‘stricte’
15, qu’on symbolisera par p 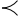 q, doubler la conjonction assertorique par une conjonction simplement problématique appelée
‘consistance’
, qu’on symbolisera par p
q, doubler la conjonction assertorique par une conjonction simplement problématique appelée
‘consistance’
, qu’on symbolisera par p 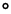 q, etc. Seulement, on s’aperçoit bientôt que, malgré les analogies de fonction entre les connecteurs des deux systèmes, l’intervention
des nuances modales transforme, quand on passe de l’un à l’autre, la structure des relations entre les divers connecteurs,
de sorte qu’on ne peut se contenter de calquer le second système sur le premier.
q, etc. Seulement, on s’aperçoit bientôt que, malgré les analogies de fonction entre les connecteurs des deux systèmes, l’intervention
des nuances modales transforme, quand on passe de l’un à l’autre, la structure des relations entre les divers connecteurs,
de sorte qu’on ne peut se contenter de calquer le second système sur le premier.
Il est naturellement possible de disposer en forme de carré les quatre jonctions et les quatre implications modales, mais
aucun de ces deux carrés ne forme un quaterne, au sens que nous avons donné à ce terme pour qu’il exprime avec précision les
rapports entre ses différents postes, c’est-à-dire pour qu’il comporte une différenciation entre contraires et subcontraires,
entre subalternants et subalternés. Avec les carrés modaux, en effet, seules subsistent les relations diagonales des contradictoires,
remarque faite que la négation d’une apodictique donne une problématique et réciproquement. La diversification entre contraires
et subcontraires s’y est effacée. Ainsi le rapport entre p 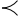 q et p
q et p 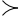 q ne peut être assimilé ni à un rapport entre contraires, puisque les deux formules peuvent être vraies ensemble, comme lorsqu’elles
se conjoignent dans la double implication ou équivalence, ni à un rapport entre subcontraires, puisque, contrairement à ce
qui se passe pour leurs correspondants assertoriques, elles peuvent aussi bien être fausses ensemble, à savoir lorsque les
deux propositions p et q sont indépendantes, n’ont pas de lien logique entre elles. Et de même avec les jonctions. Il n’y a pas incompatibilité, c’est-à-dire
exclusion de leur commune vérité, entre la conjonction problématique ou consistance (possibilité de p · q) et le rejet problématique (possibilité de ¬p · ¬q): il est possible qu’un nombre pris au hasard soit divisible à la fois par 2 et par 3, mais possible aussi qu’il ne soit
ni [147] l’un ni l’autre. Et par suite les négations de ces deux connecteurs, à savoir l’incompatibilité apodictique ou inconsistance
(impossibilité de p · q) et la disjonction apodictique (impossibilité de ¬p · ¬q) peuvent être fausses ensemble. Mais elles peuvent aussi être toutes les deux vraies: il est également impossible qu’un entier
soit pair et impair, et qu’il ne soit ni l’un ni l’autre. Par suite leurs négations, qui nous ramènent à la conjonction et
au rejet problématiques, peuvent être toutes les deux fausses. Cette absence de différenciation entre contraires et subcontraires
a naturellement pour effet, les rapports de négation contradictoire étant maintenus, de supprimer toute différenciation entre
subalternantes et subalternées.
q ne peut être assimilé ni à un rapport entre contraires, puisque les deux formules peuvent être vraies ensemble, comme lorsqu’elles
se conjoignent dans la double implication ou équivalence, ni à un rapport entre subcontraires, puisque, contrairement à ce
qui se passe pour leurs correspondants assertoriques, elles peuvent aussi bien être fausses ensemble, à savoir lorsque les
deux propositions p et q sont indépendantes, n’ont pas de lien logique entre elles. Et de même avec les jonctions. Il n’y a pas incompatibilité, c’est-à-dire
exclusion de leur commune vérité, entre la conjonction problématique ou consistance (possibilité de p · q) et le rejet problématique (possibilité de ¬p · ¬q): il est possible qu’un nombre pris au hasard soit divisible à la fois par 2 et par 3, mais possible aussi qu’il ne soit
ni [147] l’un ni l’autre. Et par suite les négations de ces deux connecteurs, à savoir l’incompatibilité apodictique ou inconsistance
(impossibilité de p · q) et la disjonction apodictique (impossibilité de ¬p · ¬q) peuvent être fausses ensemble. Mais elles peuvent aussi être toutes les deux vraies: il est également impossible qu’un entier
soit pair et impair, et qu’il ne soit ni l’un ni l’autre. Par suite leurs négations, qui nous ramènent à la conjonction et
au rejet problématiques, peuvent être toutes les deux fausses. Cette absence de différenciation entre contraires et subcontraires
a naturellement pour effet, les rapports de négation contradictoire étant maintenus, de supprimer toute différenciation entre
subalternantes et subalternées.
Pour retrouver avec les connecteurs modaux notre structure quaternaire, il faut former un quaterne mixte, où se combinent jonctions et implications. Une telle combinaison, avec toutes les propriétés formelles de la structure quaternaire, eût été déjà possible avec les connecteurs assertoriques. Si néanmoins nous ne l’avons pas retenue, c’est que, quand on cherche à articuler entre eux les deux quaternes mixtes ainsi obtenus, on se voit contraint de mettre aux deux postes de liaison ces pseudo-binaires que sont les connecteurs dégénérés, et par suite de laisser échapper l’indispensable couple de l’équivalence et de l’alternative. Avec les connecteurs modaux, où l’on dispose toujours, théoriquement, de huit termes, deux configurations mixtes sont possibles, qui satisfont l’une et l’autre aux relations caractéristiques de notre structure quaternaire. Nous préférerons naturellement retenir celle qui réunit, modalisées, la conjonction et l’implication, qui nous sont apparues, en tant que cellules originaires de chacun des quaternes, comme leur pièce maîtresse; et nous négligerons celle qui les omet, tandis qu’elle accueille certains connecteurs dont la logique modale fait si peu usage qu’elle n’a pas jugé utile de leur assigner un symbole, comme c est le cas pour les correspondants de la disjonction et du rejet. Notre quaterne se disposerait alors de la façon suivante (où les symboles de la colonne de droite se comprennent d’eux-mêmes):
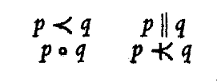
On remarquera aussitôt que, pour présenter correctement les relations caractéristiques, ce quaterne doit renverser la position de son correspondant assertorique, lequel se présenterait ainsi:
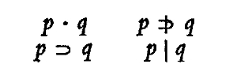
Si, dans le système modal, l’implication passe en première ligne et rejette la conjonction à la seconde, cela tient à ce que l’implication modale monte au niveau apodictique, tandis que la conjonction modale descend au niveau problématique, et que l’ordre de consécution des modales va de l’apodictique au problématique, sans réciprocité. D’où cette conséquence. Tandis que, sur le plan assertorique, la conjonction nous a paru avoir le rang prioritaire, sur le plan modal au contraire c’est l’implication qui, prenant le pas sur la conjonction, occupe la place noble. D’autres considérations, qu’il serait trop long d’exposer ici, nous paraissent d’ailleurs confirmer cette prééminence que prend, dans ce nouveau domaine, l’implication, et que méconnaissent le plus souvent les constructeurs des systèmes modaux qui, pour des raisons parfaitement valables du point de vue formel qui est le leur, prennent la consistance, conjonction problématique, comme notion première de leur système.
8
On vérifiera aisément que les quatre termes du quaterne modal mixte, ainsi renversé, soutiennent entre eux les rapports non
seulement des contradictoires, mais aussi bien des contraires, des subcontraires et des subalternes. Maintenant, ce quaterne
se prête-t-il à être lui aussi développé en une structure hexadique, par disjonction de ses postes A et E, et conjonction
de ses postes I et O? Avec la première de ces opérations, on obtient [Note: On admettra, pour simplifier l’écriture symbolique, que les symboles modaux lient plus fortement que ceux des connecteurs
assertoriques.] p 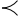 q ∨ p
q ∨ p 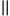 q, ce qui représente le cas de deux propositions p et q entre lesquelles il y a un lien logique de dépendance, positive ou négative: soit que l’une des propositions entraîne nécessairement
l’autre, soit qu’au contraire les deux s’excluent mutuellement. Avec la seconde, on obtient naturellement la négation du résultat
de la première, soit p
q, ce qui représente le cas de deux propositions p et q entre lesquelles il y a un lien logique de dépendance, positive ou négative: soit que l’une des propositions entraîne nécessairement
l’autre, soit qu’au contraire les deux s’excluent mutuellement. Avec la seconde, on obtient naturellement la négation du résultat
de la première, soit p 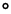 q · p
q · p  q, ce qui représente le cas de deux propositions qui sont à la fois compatibles et indépendantes, c’est-à-dire telles que les
seules ressources de la logique ne permettent pas de conclure, affirmativement ou négativement, de l’une à l’autre.
q, ce qui représente le cas de deux propositions qui sont à la fois compatibles et indépendantes, c’est-à-dire telles que les
seules ressources de la logique ne permettent pas de conclure, affirmativement ou négativement, de l’une à l’autre.
On ne s’étonnera pas si l’hexagone ainsi construit sur les connecteurs modalisés se superpose exactement à celui qui se laisse construire sur les notions modales elles-mêmes. On connaît depuis longtemps l’analogie entre le carré des quatre modalités dites aristotéliciennes (nécessaire, impossible, possible au sens de pur possible, contingent au sens de non-nécessaire) avec le traditionnel carré des quantificateurs qui sert toujours de référence. La correspondance se poursuit avec la transformation du carré en hexagone. Cette transformation a pour effet, dans le cas des notions modales, d’assigner une place précise, par l’institution d’un poste Y, à la notion de ce qui est à la fois possible et contingent; ce qui a l’avantage, d’abord de dégager explicitement une notion qui nous est, en fait, d’usage plus courant que les deux qu’elle conjoint prises séparément, ensuite et par voie de conséquence de faciliter la levée de l’ambiguïté dont souffrent les mots de possible et de contingent qui, en raison même du besoin que nous avons d un mot pour l’idée usuelle qui les conjoint, ont tendance à osciller entre leur sens unilatéral [149] I ou O et le sens bilatéral Y, créant ainsi des confusions et des distorsions. On pourra, pour prévenir l’amphibologie et rétablir la symétrie, qualifier d’éventuel ce qui ainsi peut être niais peut aussi ne pas être, ce qui n’est ni impossible ni nécessaire, et contenir alors les mots de possible et de contingent dans le sens unilatéral qu’ils prennent aux postes I et O, et qui permet de les distinguer nettement.
Avec les connecteurs modalisés, le même besoin se fait sentir d’une notion qui enveloppe à la fois celle de l’indépendance et celle de la compatibilité des propositions. En fait, là aussi, nous pensons le plus souvent ces notions dans leur conjonction, même si l’une des deux demeure à l’arrière-plan. De deux propositions dont l’une implique strictement l’autre, il nous paraîtra superflu de dire qu’elles sont compatibles. Nous emploierons donc en général ce dernier mot pour désigner les couples de propositions qui sont, aussi, indépendantes, même si cette dernière notion reste alors, comme c’est ordinairement le cas, sous-entendue. Là aussi, il faut éviter que les habitudes du vocabulaire nous masquent l’organisation conceptuelle authentique, ce que permet la reconnaissance expresse, du côté des problématiques, d’un troisième poste Y appelant avec lui, comme son opposé diamétral du côté des apodictiques, sa négation contradictoire en U.
Ce ne sont donc pas seulement des raisons d’analogie, ou de régularité esthétique, qui nous font organiser les connecteurs modaux en cette structure hexadique. On remarquera que le triangle des contraires AYE, loin d’être une construction artificielle, fausse fenêtre pour la symétrie d’ensemble du système, correspond exactement aux trois situations dans lesquelles, du point de vue de leur rapport logique, peuvent se trouver deux propositions: ou bien connexion nécessaire (A), ou bien exclusion nécessaire (E), ou bien ni l’un ni l’autre, c’est-à-dire possibilité d’être ou non posées ensemble (Y). Ou si, afin de ne pas laisser de côté le terme en U, l’on préfère considérer le couple de contradictoires UY, on voit que l’alternative qu’il présente est tout à fait essentielle du point de vue logique, puisque c’est précisément celle de la présence ou de l’absence d’un rapport logique entre deux propositions.
Notes
1. Karl Dôhmann, ‘Der Gruppencharakter der Transformationen der dyadischen Aussage-Verknüpfungen’, Logique et Analyse, no. 38, juin 1967, p. 218-228. ↵
2. Jean Piaget, Traité de Logique, 1949. p. 272, quaterne B. ↵
3. W. H. Gottschalk, ‘The theory of quaternality’, Journal of Symbolic Logic, 1953, p. 193-196. ↵
4. Avec les indices nécessaires: ΦN, ΦD, ΦC. A vrai dire, Φ symbolise une formule quelconque du calcul des propositions; mais cela revient, pour notre propos, à symboliser le connecteur principal de cette formule, puisqu’il est la seule variable quand on passe d’un coin du carré à l’autre. ↵
5. Plus exactement, des opérations interpropositionnelles; mais comme celles-ci sont commandées par les opmteurs correspondants, qui sont les connecteurs, la transposition est permise. ↵
6. C’est également ce groupe que retrouve Döhmann dans l’étude à laquelle nous nous référions tantôt. ↵
7. Nous reprenons ici, mais sous une forme diffërente, comportant quelques suppressions ou condensations, et quelques additions ou développements, l’essentiel de ce que nous avons exposé dans Structures intellectuelles (Vrin, 1966), chap. IX, et dans Raison et discours (ibid., 1967), chap. VII, §20. ↵
8. Journal of Symbolic Logic, 195" p. 16.2. ↵
9. J. Dopp, Leçons de logique formelle, Louvain, 1950, vol. II, p. 67, qui ajoute ce commentaire: “On voit donc que l’idée de ‘fonction’ dont nous sommes partis doit être prise en un sens assez large pour s’appliquer au cas d’expressions dont la valeur ne varie pas lorsque varie la valeur des variables qu’elles mentionnent. C’est là, au reste, un procédé d’élargissement de notions qui est fréquemment pratiqué dans les sciences modernes.” ↵
10. H. Reichenbach, Elements of Symbolic Logic, New York, 1947, p. 34-35. ↵
11. Ouv. cité, p. 267. ↵
12. On sait que p ⊃ q · ≡ · ¬(p · ¬q), etc. On remarquera que le dernier carré apparaît sens dessus dessous par rapport au premier, puisque son élément générateur, Il savoir l’implication, se trouve situé sur la seconde ligne, au lieu de figurer, comme était la conjonction, sur la première. On comprendra plus loin la signification de ce renversement. ↵
13. Là encore, on comprendra plus loin la signification de cette permutation. ↵
14. A. Church, Introduction to mathematical logic, vol. l, Princeton, 1956, p. 102. ↵
15. A vrai dire, l’implication stricte de Lewis ne coïncide pas exactement, comme il l’avait cru d’abord, avec la relation de conséquence logique; elle s’en rapproche cependant beaucoup plus, en raison de son podicité, que ne fait la simple implication assertorique. ↵
Editorial Notes
i. Within the text as it was originally published, Blanché marks the negation of a logical value by means of a bar or over-line. For ease of transcription, however, in this HTML version of the article the character ‘¬’ has been used instead, combined with parentheses where appropriate. For more information, see: http://en.wikipedia.org/wiki/Negation. ↵
