Synopsis of Robert Blanché, ‘Sur le système des connecteurs interpropositionnels’
[‘On the System of Interpropositional Connectors’]
CpA 10.7:131–149
The logician Robert Blanché (1898-1975) taught at the University of Toulouse. A prolific writer, he was the author of some twenty volumes, including works on many of the topics of interest to the editors of the Cahiers pour l'Analyse: axiomatics (1955), ‘intellectual structures’ (1966), rationalism, epistemology, as well as the relations between logic, mathematics and the physical sciences. Blanché was already a well-established figure and nearing the end of his career when his contribution to the Cahiers was published, in its final volume.
Though he was an important and original thinker, Blanché's work remains little known in English, and even in France his specialisation in logic served to isolate him, to some extreme, from the mainstream philosophical community. For centuries, French philosophers tended to follow Descartes' devaluation of logic per se as secondary in relation to forms of reasoning modelled on mathematics itself; French mathematicians like Henri Poincaré subsequently came to share a similar scorn for the discipline. As it stands, Blanché is best known in France for his relatively conventional textbook on the history of logic (1970), and his more original contributions to the field are rarely read either in France or abroad.
As its title implies, Blanché's major work, Structures intellectuelles (1966), situates him squarely in the structuralist camp, alongside Bourbaki and Lévi-Strauss. As with other structuralist thinkers, Blanché assumes that we can only understand a given term or concept through the relation it has with other terms. Structures intellectuelles presents, among other things, an expanded and refined (‘hexagonal’) model of the traditional square of logical oppositions (see below). In his contribution to the Cahiers, Blanché applies his hexagonal model to the classification of the propositional connectives or connectors used in classical logic. As the term implies, connectives (used together with quantifiers, variables and predicates) serve to make new propositions by combining others, for instance by negation, conjunction, or implication. The natural language equivalent for such connectives include terms like ‘and’, ‘or’, ‘if’, ‘therefore’, ‘however’, and so on; formal logic allows such relations to be articulated more precisely, and provides conventional notation to express negation (¬), implication (→ or ⊃), disjunction (∨) conjunction (∧ or ⋅) and equivalence (↔).1
Blanche's article is the most technical and specialised discussion of logic published in the whole of the Cahiers. It serves as a bridge, in effect, between some of the points raised by Jacques Brunschwig's discussion of Aristotelian syllogism in (CpA 10.1) and the canonical texts on modern logic collected in the rest of Cahiers volume ten. Blanché's main discovery here was first presented in summary form in 1957, in a brief, two-page text published in the Journal of Symbolic Logic.2 Blanché was not the first logician to try to organise or ‘structure’ the connectives of classical propositional logic in a systematic way; the problem was previously tackled by Jean Piaget (1949) and then by W.H. Gottschalk (1953). In the first two numbered sections of his Cahiers article, Blanché presents and criticizes these previous efforts in some detail, after providing an initial critique of Karl Döhmann's more recent (1967) contribution to the question.3
Blanché's text presumes familiarity with the ‘traditional square of opposition’, originally derived from Aristotle (De Interpretatione 6–7). The set of logical relationships codified in this conventional diagram, notes Terence Parsons, ‘provided a foundation for work in logic for over two millennia.’4 There are many different versions of the square, but the following configuration of logical quantifiers (‘every’ , ‘no’, ‘some’ and ‘some-not’ or ‘not-all’) is closely connected with Aristotle's own ideas and examples.
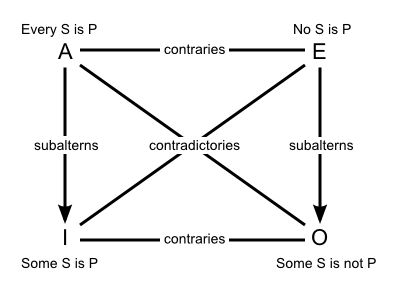
The square is based on three relations of opposition and the additional relation of subalternation. Two propositions can be classified as contraries if together they cannot be true, as subcontraries if together they cannot be false, and contradictories if together they cannot be either true or false. Subalternation is just another way of expressing implication (if... then...).
To better visualise the square it may be useful to represent these relations with colours: red for contradictories, blue for contraries, green for subcontraries and black for subalternation. The corners of the square are traditionally designated, via Latin abbreviations, by the four letters A, E, I, O. This gives us the following basic diagram, used here to express the various logical relations between the subject ‘men’ and the predicate ‘white’:
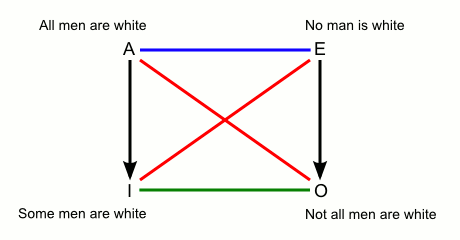
In spite of its appealing symmetry and economy, there are some significant problems with the traditional square: the meaning of ‘some’ in the I-corner does not overlap unequivocally with the natural language uses of some, and there is no clear expression or name for the 0-corner (‘some’ as ‘not all’) in any natural language (see Horn, 1989, 2010). As a result, in the mid-nineteenth century some logicians began to replace the square by a triangle in which there is only one notion of opposition (contrariety):
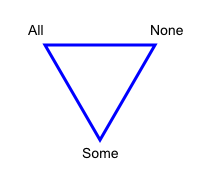
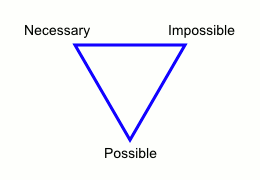
The same configuration was also used for logical modalities (see Gardies 1979):
Blanché's own variation on the traditional square solves the problem of the I and O corners by replacing the square not with a triangle but with a hexagon (itself the product of two triangles).5 Used to express connections between the logical quantifiers, this yields the following diagram:
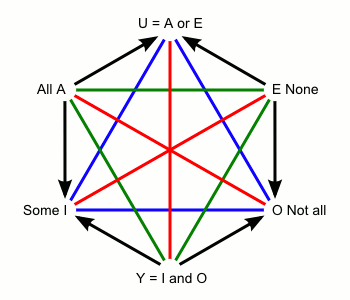
And then for the modalities:
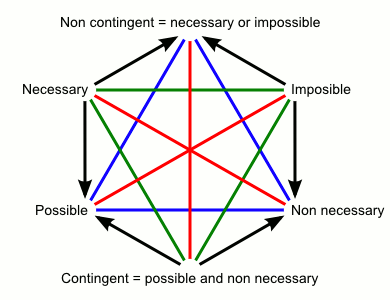
Blanché's goal, in his Cahiers article, is to use his hexagonal configuration as a complete and unambiguous way of formalising the set of possible logical relations that exist between two propositions. Given two propositions P and Q, classical formal logic recognises sixteen variations on their possible connection (including contradiction, conjunction, converse non-implication, and so on).6 The clearest and most familiar way of formalising these relations (which Blanché himself takes for granted here) is to consider the sixteen possible ways of writing a four-digit binary sequence (i.e. four-digit combinations of 0s and 1s), where P can be used to represent {0,0,1,1} and Q to represent {0,1,0,1}. The sixteen possible arrangements of such a sequence can be made to correspond to the sixteen binary connectives of classical propositional logic, along the lines summarised in this table:
| p | q | ¬p | ¬q | p∧q | p∨q | ¬p∧q | p∧¬q | ¬p∧¬q | ¬p∨q | p∨¬q | ¬p∨¬q | p↔q | ¬(p↔q) |
| ¬(p←q) | ¬(p→q) | ¬(p∨q) | p→q | p←q | ¬(p∧q) | ||||||||
| p·q | p∨q |
p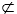 q q
|
p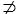 q q
|
p∧q | p⊃q | p⊂q | p|q | p≡q |
p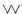 q q
|
||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
The top line here corresponds to the most standard names for the connectives, i.e. the names which are most often used by contemporary logicians. The second line lists some useful alternative names for some of the binary connectives (these are the names we will use in the diagrammatic representations below). The third line lists Blanché's own notation. Note that we have only included fourteen columns in this table: the columns that include only 0s and only 1s do not appear. The first four columns can also be considered as ‘degenerate’ [dégénérés] and insignificant cases, as Blanché points out, since they are not really binary connectives (i.e. relations between P and Q).
So as far as the binary logical connectives are concerned, we are thus left with the following ten columns (where again, the third line corresponds to Blanché's terminology):
| p∧q | p∨q | ¬p∧q | p∧¬q | ¬p∧¬q | ¬p∨q | p∨¬q | ¬p∨¬q | p↔q | ¬(p↔q) |
| ¬(p←q) | ¬(p→q) | ¬(p∨q) | p→q | p←q | ¬(p∧q) | ||||
| p·q | p∨q |
p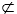 q q
|
p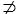 q q
|
p∧q | p⊃q | p⊂q | p|q | p≡q |
p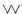 q q
|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
Piaget and Gottschalk, Blanché notes, didn't deal with the last two columns. They both developed an alternative square of opposition based on four of the eight middle connectives. What Blanché does in the central part of his article (sections 3 to 6) is reconstruct these two squares, transforming them into two hexagons and incorporating in addition the connectives defined by the last two columns.
Here now is the resulting full diagram presented by Blanché on page 144, with the connectives renamed in line with standard logical notation:
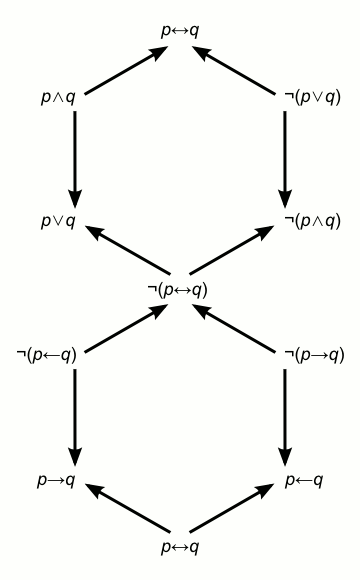
To provide a better understanding of Blanché's construction we can present the same diagram using full hexagons and colours (again red for contradictories, blue for contraries, green for subcontraries and black for subalternation).
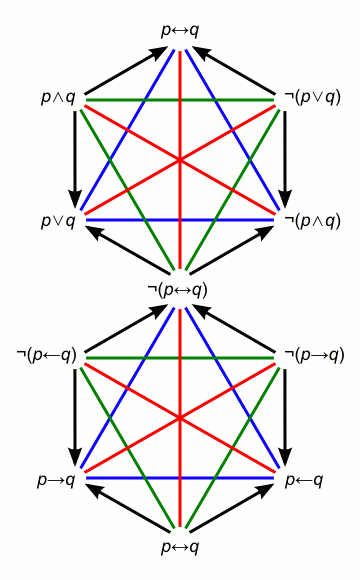
The last two sections (7-8) of Blanche's paper suggests how we might extend this new configuration to the domain of modal logic. Blanché's argument is again highly technical, and somewhat schematic: basically, he proposes to redesign the second hexagon (the implicative hexagon) by replacing material implication with strict implication.
References to this text in other articles in the Cahiers pour l’Analyse:
None.
English translation:
None.
Primary bibliography:
- Anellis, Irving. Logic and its History in the Work and Writings of Jean van Heijenoort. Ames, Iowa: Modern Logic, 1994.
- Blanché, Robert. L’Axiomatique. Paris: PUF, 1955.
- ---. ‘Sur l'opposition des concepts’. Theoria 19 (1953): 89-130.
- ---. ‘Sur la structuration du tableau des connectifs interpropositionnels binaires’. Journal of Symbolic Logic 22:1 (1957): 17-18.
- ---. Structures intellectuelles. Essai sur l'organisation systématique des concepts. Paris: Vrin, 1966.
- ---. La Logique et son histoire, d'Aristote à Russell. Paris: Armand Collin, 1970.
- Feferman, Anita B. From Trotsky to Gödel –The life of Jean van Heijenoort [second edition]. Wellesley MA: A. K. Peters, 2008.
- Gardies, Jean-Louis. Essai sur la logique des modalités. Paris: PUF, 1979.
- Heijenoort, Jean van. Review of Blanché, ‘Sur la structuration du tableau des connectifs interpropositionnels binaires’ [1957]. Journal of Symbolic Logic 24:3 (1959): 228.
- Horn, Laurence. A Natural History of Negation. Chicago: University of Chicago Press, 1989.
- ---. ‘Histoire d'*0’. In New Perspectives on the Square of Opposition, ed. Jean-Yves Béziau and Gillman Payette. Berne: Peter Lang, 2010.
Selected secondary literature:
- Béziau, Jean-Yves. ‘New Light on the Square of Opposition and its Nameless Corner’. Logical Investigations 10 (2003): 218-232.
- Béziau, Jean-Yves, and Gillman Payette, eds. Logica Universalis 2:1 (2008). Special issue on the Square of Opposition.
- Moretti, Alessio. The Geometry of Logical Opposition. PhD Thesis, University of Neuchâtel, Switzerland, 2009.
Notes
1. For more information see ‘Logical Connective’, Wikipedia, http://en.wikipedia.org/wiki/Logical_connective, ‘Classical Logic’, Stanford Encyclopaedia of Philosophy, http://plato.stanford.edu/entries/logic-classical/, and ‘Logical Constants’, Stanford Encyclopaedia of Philosophy, http://plato.stanford.edu/entries/logical-constants/. ↵
2. Blanché's 1957 paper didn't receive much attention but it was reviewed by another remarkable French logician, the Trotskyist Jean van Heijenoort, in 1959, also in the Journal of Symbolic Logic. ↵
3. Karl Döhmann, ‘Der Gruppencharakter der Transformation der dyadischen Aussage-Verknüpfungen’, Logique et Analyse 38 (June 1967), 218-228. ↵
4. Terence Parsons, ‘The Traditional Square of Opposition’, Stanford Encyclopaedia of Philosophy, http://plato.stanford.edu/entries/square/. ↵
5. Thanks to its rough shape on the map of Europe, France itself is colloquially known as l'hexagone. ↵
6. The complete set of these sixteen relations is represented, in a variety of formats, under the heading ‘Table of binary logical connectives’, at http://en.wikipedia.org/wiki/Logical_connective. ↵
